遍历二叉树 - 基于栈的DFS

之前已经学过二叉树的DFS的遍历算法【http://www.cnblogs.com/webor2006/p/7244499.html】，当时是基于递归来实现的，这次利用栈不用递归也来实现DFS的遍历，这里先只学习如何用它进行二叉树的前序遍历，具体何为前序遍历这里不多解释，可以参考之前写的博客有详细的说明，下面开始实现。

实现一个栈：

为了能让栈里面可以放任何类型的数据，则使用C++的模板来实现，先新建一个stack头文件，以便在我们需要用的文件中只要引用头文件既可：

然后再新建一个Stack类，里面定义栈的几个经典方法：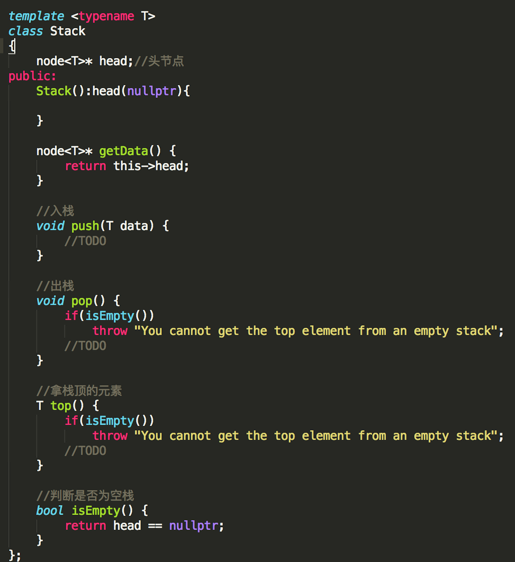

由于比较好理解，下面直接给出具体实现，不多解释：

/*
* 利用模板来实现一个栈，可以往里面添加任意一个元素
*/

template <typename T>
struct node
{
    T data;
    struct node* next;
    node(T data) {this->data = data;};
};

template <typename T>
class Stack
{
    node<T>* head;//头节点
public:
    Stack():head(nullptr){

    }

    node<T>* getData() {
        return this->head;
    }

    //入栈
    void push(T data) {
        node<T>* new_node = new node<T>(data);
        new_node->next = head;
        head = new_node;
    }

    //出栈
    void pop() {
        if(isEmpty())
              throw "You cannot get the top element from an empty stack";
          node<T>* temp = head;
          head = temp->next;
          delete temp;
    }

    //拿栈顶的元素
    T top() {
        if(isEmpty())
              throw "You cannot get the top element from an empty stack";
          return head->data;
    }

    //判断是否为空栈
    bool isEmpty() {
        return head == nullptr;
    }
};

下面来使用一下咱们实现的Stack，如下：

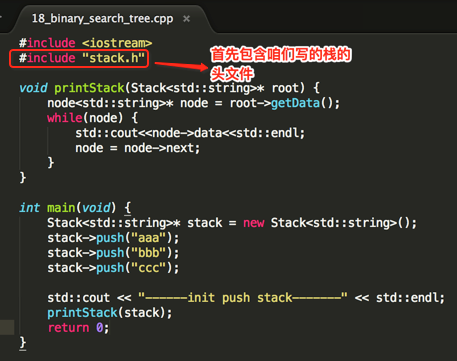
编译运行：

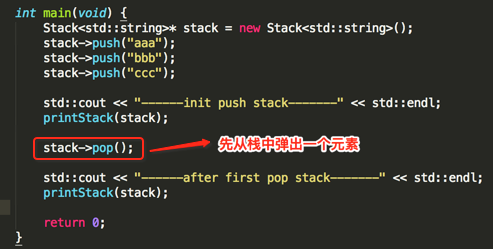
编译运行：

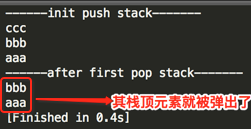
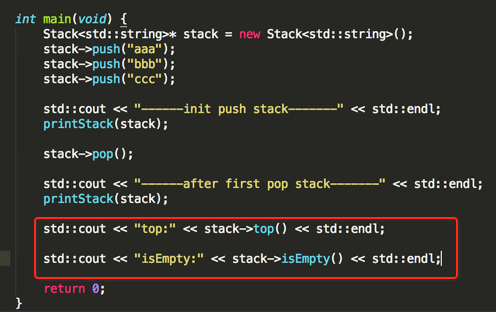
编译运行：

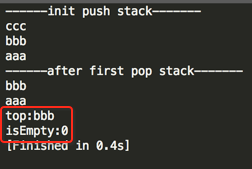
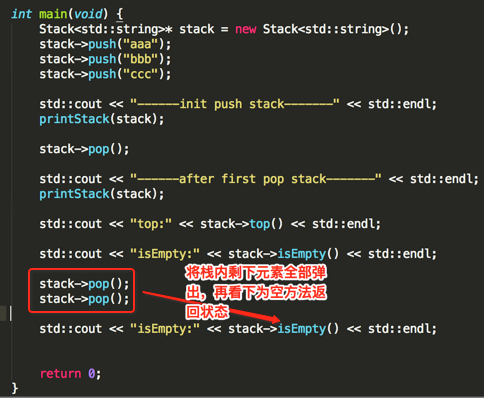
编译运行：

ok，一切如预期~

利用栈构建一个二叉树：

新建一个结构体用来构造二叉树：

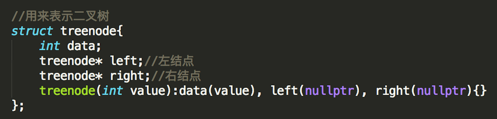
接着用它来构建一个二叉树，还是构建之前已经使用过的如下二叉树：

下面开始构建：

利用栈对二叉树进行前序遍历：

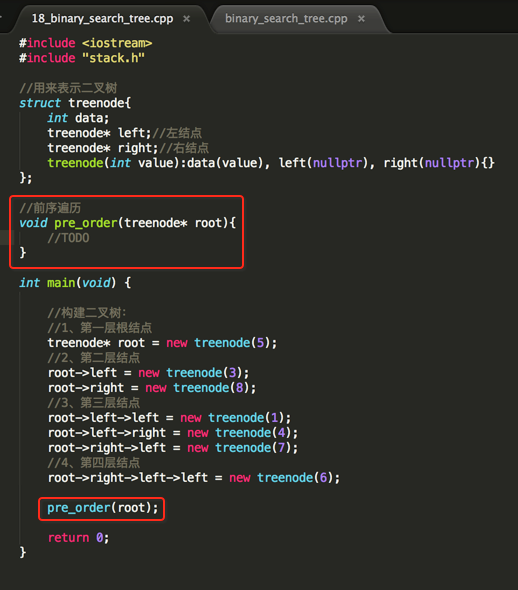
下面看下具体实现：

#include <iostream>
#include "stack.h"

//用来表示二叉树
struct treenode{
    int data;
    treenode* left;//左结点
    treenode* right;//右结点
    treenode(int value):data(value), left(nullptr), right(nullptr){}
};

//前序遍历
void pre_order(treenode* root){
    Stack<treenode*> stack;//声明一个栈
    treenode* current_node = root;
    while(current_node) {
        //1、首先打印当前结点，因为是前序遍历
        std::cout << current_node->data << std::endl;
        //2、如果存在右结点则将其入栈暂存,待左结点输出完之后再去处理这些右结点
        if(current_node->right) stack.push(current_node->right);
        //3、不断去处理左结点，直到左结点处理完了，则从栈中拿右点进行处理
        if(current_node->left)//如果有左结点，则将它做为当前处理的结点不断输出
            current_node = current_node->left;
        else {
            //这时左结点已经处理完了
            if(stack.isEmpty())//如果缓存栈已经为空了则说明整个二叉树的遍历结束了
                current_node = nullptr;
            else {
                //则取出栈顶的右结点进行处理，由于是后进先出，所以拿出来的永远是最新插入的右结点
                current_node = stack.top();
                stack.pop();//将其元素从栈顶弹出
            }

        }
    }
}

int main(void) {

    //构建二叉树：
    //1、第一层根结点
    treenode* root = new treenode();
    //2、第二层结点
    root->left = new treenode();
    root->right = new treenode();
    //3、第三层结点
    root->left->left = new treenode();
    root->left->right = new treenode();
    root->right->left = new treenode();
    //4、第四层结点
    root->right->left->left = new treenode();

    pre_order(root);

    return ;
}

可见其遍历过程并未用到递归，编译运行：

Debug分析：

root = new treenode(5);

①、，新建一个栈，用来存放暂存的结点。

②、

③、开始进行循环遍历：

Loop1: current_node = new treenode(5);

　　a、打印当有结点【5】。

　　b、current_node->right = new treenode(8);条件为真，则将它添加入栈暂存。此是栈为：
　　　　

　　c、current_node->left = new treenode(3);有左结点，条件为真,current_node = new treenode(3);

Loop2:current_node = new treenode(3);

　　a、打印当有结点【3】。

　　b、current_node->right = new treenode(4);条件为真，则将它添加入栈暂存。此是栈为：

　　　　

　　c、current_node->left = new treenode(1);有左结点，条件为真,current_node = new treenode(1);

Loop3:current_node = new treenode(1);

　　a、打印当有结点【1】。

　　b、current_node->right = null;条件为假，继续c：

　　c、current_node->left = null;木有左结点，条件为假,执行d；

　　d、这时左结点已经处理完，则从栈中去处理右结点

　　　　①、当前栈不为空，条件不满足执行②。

　　　　②、取出栈顶的右结点进行处理：current_node = new treenode(4);并将这上结点从栈中弹出。

Loop4:current_node = new treenode(4);

　　a、打印当有结点【4】。

　　b、current_node->right = null;条件为假，继续c：

　　c、current_node->left = null;木有左结点，条件为假,执行d；

　　d、这时左结点已经处理完，则从栈中去处理右结点

　　　　①、当前栈不为空，条件不满足执行②。

　　　　②、取出栈顶的右结点进行处理：current_node = new treenode(8);并将这上结点从栈中弹出。

Loop5:current_node = new treenode(8);

　　a、打印当有结点【8】。

　　b、current_node->right = null;条件为假，继续c：

　　c、current_node->left = new treenode(7);有左结点，条件为真,current_node = new treenode(7);

Loop6:current_node = new treenode(7);

　　a、打印当有结点【7】。

　　b、current_node->right = null;条件为假，继续c：

　　c、current_node->left = new treenode(6);有左结点，条件为真,current_node = new treenode(6);

Loop7:current_node = new treenode(6);

　　a、打印当有结点【6】。

　　b、current_node->right = null;条件为假，继续c：

　　c、current_node->left = null;木有左结点，条件为假,执行d；

　　d、这时左结点已经处理完，则从栈中去处理右结点

　　　　①、当前栈为空，条件满足，current_node = null;

Loop8:current_node = null;其循环条件不满足退出循环。

复杂度分析：

时间复杂度：由于每个结点都会循环到，所以说它的复杂度是O(N)。

空间复杂度：从上面的debug分析结果可以看出，栈中最多只会存树的深度大小，所以说空间复杂度正常情况下是：O(logN);除非是一个极端的二叉树，结点都放到一边了，那最差也是O(N)。