题目要求

建立房价预测模型：利用ex1data1.txt（单特征）和ex1data2.txt（多特征）中的数据，进行线性回归和预测。

作散点图可知，数据大致符合线性关系，故暂不研究其他形式的回归。

两份数据放在最后。

单特征线性回归

ex1data1.txt中的数据是单特征，作一个简单的线性回归即可：\(y=ax+b\)。

根据是否分割数据，产生两种方案：方案一，所有样本都用来训练和预测；方案二，一部分样本用来训练，一部分用来检验模型。

方案一

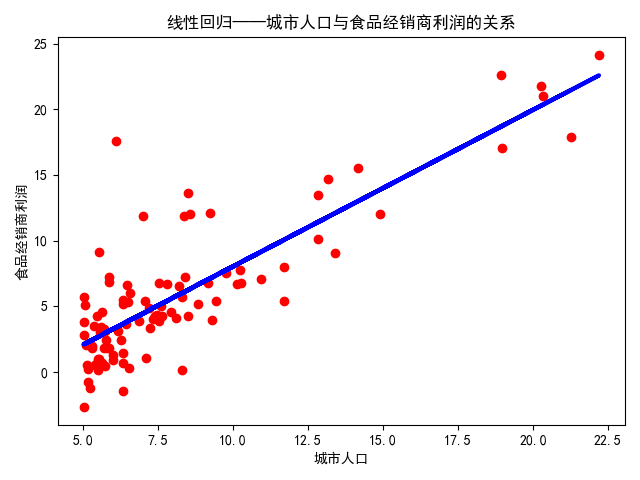
对ex1data1.txt中的数据进行线性回归，所有样本都用来训练和预测。

代码实现如下：

  1. """
  2.     对ex1data1.txt中的数据进行线性回归，所有样本都用来训练和预测
  3. """
  4. import numpy as np
  5. import matplotlib.pyplot as plt
  6. from sklearn.linear_model import LinearRegression
  7. from sklearn.metrics import mean_squared_error, r2_score
  8. plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
  9. plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
  11. # 数据格式：城市人口,食品经销商利润
  13. # 读取数据
  14. data = np.loadtxt('ex1data1.txt', delimiter=',')
  15. data_X = data[:, 0]
  16. data_y = data[:, 1]
  18. # 训练模型
  19. model = LinearRegression()
  20. model.fit(data_X.reshape([-1, 1]), data_y)
  22. # 利用模型进行预测
  23. y_predict = model.predict(data_X.reshape([-1, 1]))
  25. # 结果可视化
  26. plt.scatter(data_X, data_y, color='red')
  27. plt.plot(data_X, y_predict, color='blue', linewidth=3)
  28. plt.xlabel('城市人口')
  29. plt.ylabel('食品经销商利润')
  30. plt.title('线性回归——城市人口与食品经销商利润的关系')
  31. plt.show()
  33. # 模型参数
  34. print(model.coef_)
  35. print(model.intercept_)
  36. # MSE
  37. print(mean_squared_error(data_y, y_predict))
  38. # R^2
  39. print(r2_score(data_y, y_predict))

结果如下：

由下可知函数形式以及\(R^2\)为0.70

  1. [1.19303364]
  2. -3.89578087831185
  3. 8.953942751950358
  4. 0.7020315537841397

方案二

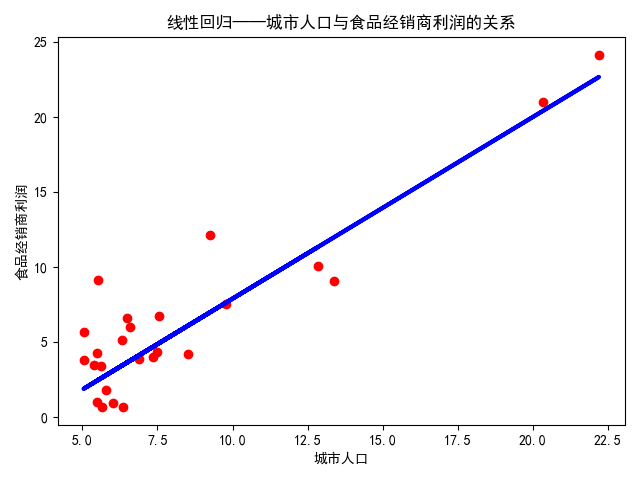
对ex1data1.txt中的数据进行线性回归，部分样本用来训练，部分样本用来预测。

实现如下：

  1. """
  2.     对ex1data1.txt中的数据进行线性回归，部分样本用来训练，部分样本用来预测
  3. """
  4. import numpy as np
  5. import matplotlib.pyplot as plt
  6. from sklearn.linear_model import LinearRegression
  7. from sklearn.model_selection import train_test_split
  8. from sklearn.metrics import mean_squared_error, r2_score
  9. plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
  10. plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
  12. # 数据格式：城市人口,食品经销商利润
  14. # 读取数据
  15. data = np.loadtxt('ex1data1.txt', delimiter=',')
  16. data_X = data[:, 0]
  17. data_y = data[:, 1]
  19. # 数据分割
  20. X_train, X_test, y_train, y_test = train_test_split(data_X, data_y)
  22. # 训练模型
  23. model = LinearRegression()
  24. model.fit(X_train.reshape([-1, 1]), y_train)
  26. # 利用模型进行预测
  27. y_predict = model.predict(X_test.reshape([-1, 1]))
  29. # 结果可视化
  30. plt.scatter(X_test, y_test, color='red')  # 测试样本
  31. plt.plot(X_test, y_predict, color='blue', linewidth=3)
  32. plt.xlabel('城市人口')
  33. plt.ylabel('食品经销商利润')
  34. plt.title('线性回归——城市人口与食品经销商利润的关系')
  35. plt.show()
  37. # 模型参数
  38. print(model.coef_)
  39. print(model.intercept_)
  40. # MSE
  41. print(mean_squared_error(y_test, y_predict))
  42. # R^2
  43. print(r2_score(y_test, y_predict))

结果如下：

由下可知函数形式以及\(R^2\)为0.80

  1. [1.21063939]
  2. -4.195481965945055
  3. 5.994362667047617
  4. 0.8095125123727652

多特征线性回归

ex1data2.txt中的数据是二个特征，作一个最简单的多元（在此为二元）线性回归即可：\(y=a_1x_1+a_2x_2+b\)。

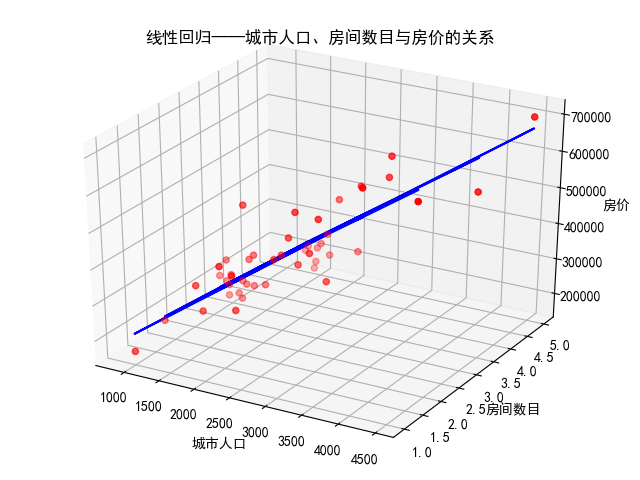
对ex1data2.txt中的数据进行线性回归，所有样本都用来训练和预测。

代码实现如下：

  1. """
  2.     对ex1data2.txt中的数据进行线性回归，所有样本都用来训练和预测
  3. """
  4. import numpy as np
  5. import matplotlib.pyplot as plt
  6. from sklearn.linear_model import LinearRegression
  7. from mpl_toolkits.mplot3d import Axes3D  # 不要去掉这个import
  8. from sklearn.metrics import mean_squared_error, r2_score
  9. plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
  10. plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
  12. # 数据格式：城市人口,房间数目,房价
  14. # 读取数据
  15. data = np.loadtxt('ex1data2.txt', delimiter=',')
  16. data_X = data[:, 0:2]
  17. data_y = data[:, 2]
  19. # 训练模型
  20. model = LinearRegression()
  21. model.fit(data_X, data_y)
  23. # 利用模型进行预测
  24. y_predict = model.predict(data_X)
  26. # 结果可视化
  27. fig = plt.figure()
  28. ax = fig.gca(projection='3d')
  29. ax.scatter(data_X[:, 0], data_X[:, 1], data_y, color='red')
  30. ax.plot(data_X[:, 0], data_X[:, 1], y_predict, color='blue')
  31. ax.set_xlabel('城市人口')
  32. ax.set_ylabel('房间数目')
  33. ax.set_zlabel('房价')
  34. plt.title('线性回归——城市人口、房间数目与房价的关系')
  35. plt.show()
  37. # 模型参数
  38. print(model.coef_)
  39. print(model.intercept_)
  40. # MSE
  41. print(mean_squared_error(data_y, y_predict))
  42. # R^2
  43. print(r2_score(data_y, y_predict))

结果如下：

由下可知函数形式以及\(R^2\)为0.73

  1. [  139.21067402 -8738.01911233]
  2. 89597.90954279748
  3. 4086560101.205658
  4. 0.7329450180289141

两份数据

ex1data1.txt

  1. 6.1101,17.592
  2. 5.5277,9.1302
  3. 8.5186,13.662
  4. 7.0032,11.854
  5. 5.8598,6.8233
  6. 8.3829,11.886
  7. 7.4764,4.3483
  8. 8.5781,12
  9. 6.4862,6.5987
  10. 5.0546,3.8166
  11. 5.7107,3.2522
  12. 14.164,15.505
  13. 5.734,3.1551
  14. 8.4084,7.2258
  15. 5.6407,0.71618
  16. 5.3794,3.5129
  17. 6.3654,5.3048
  18. 5.1301,0.56077
  19. 6.4296,3.6518
  20. 7.0708,5.3893
  21. 6.1891,3.1386
  22. 20.27,21.767
  23. 5.4901,4.263
  24. 6.3261,5.1875
  25. 5.5649,3.0825
  26. 18.945,22.638
  27. 12.828,13.501
  28. 10.957,7.0467
  29. 13.176,14.692
  30. 22.203,24.147
  31. 5.2524,-1.22
  32. 6.5894,5.9966
  33. 9.2482,12.134
  34. 5.8918,1.8495
  35. 8.2111,6.5426
  36. 7.9334,4.5623
  37. 8.0959,4.1164
  38. 5.6063,3.3928
  39. 12.836,10.117
  40. 6.3534,5.4974
  41. 5.4069,0.55657
  42. 6.8825,3.9115
  43. 11.708,5.3854
  44. 5.7737,2.4406
  45. 7.8247,6.7318
  46. 7.0931,1.0463
  47. 5.0702,5.1337
  48. 5.8014,1.844
  49. 11.7,8.0043
  50. 5.5416,1.0179
  51. 7.5402,6.7504
  52. 5.3077,1.8396
  53. 7.4239,4.2885
  54. 7.6031,4.9981
  55. 6.3328,1.4233
  56. 6.3589,-1.4211
  57. 6.2742,2.4756
  58. 5.6397,4.6042
  59. 9.3102,3.9624
  60. 9.4536,5.4141
  61. 8.8254,5.1694
  62. 5.1793,-0.74279
  63. 21.279,17.929
  64. 14.908,12.054
  65. 18.959,17.054
  66. 7.2182,4.8852
  67. 8.2951,5.7442
  68. 10.236,7.7754
  69. 5.4994,1.0173
  70. 20.341,20.992
  71. 10.136,6.6799
  72. 7.3345,4.0259
  73. 6.0062,1.2784
  74. 7.2259,3.3411
  75. 5.0269,-2.6807
  76. 6.5479,0.29678
  77. 7.5386,3.8845
  78. 5.0365,5.7014
  79. 10.274,6.7526
  80. 5.1077,2.0576
  81. 5.7292,0.47953
  82. 5.1884,0.20421
  83. 6.3557,0.67861
  84. 9.7687,7.5435
  85. 6.5159,5.3436
  86. 8.5172,4.2415
  87. 9.1802,6.7981
  88. 6.002,0.92695
  89. 5.5204,0.152
  90. 5.0594,2.8214
  91. 5.7077,1.8451
  92. 7.6366,4.2959
  93. 5.8707,7.2029
  94. 5.3054,1.9869
  95. 8.2934,0.14454
  96. 13.394,9.0551
  97. 5.4369,0.61705

ex1data2.txt

  1. 2104,3,399900
  2. 1600,3,329900
  3. 2400,3,369000
  4. 1416,2,232000
  5. 3000,4,539900
  6. 1985,4,299900
  7. 1534,3,314900
  8. 1427,3,198999
  9. 1380,3,212000
  10. 1494,3,242500
  11. 1940,4,239999
  12. 2000,3,347000
  13. 1890,3,329999
  14. 4478,5,699900
  15. 1268,3,259900
  16. 2300,4,449900
  17. 1320,2,299900
  18. 1236,3,199900
  19. 2609,4,499998
  20. 3031,4,599000
  21. 1767,3,252900
  22. 1888,2,255000
  23. 1604,3,242900
  24. 1962,4,259900
  25. 3890,3,573900
  26. 1100,3,249900
  27. 1458,3,464500
  28. 2526,3,469000
  29. 2200,3,475000
  30. 2637,3,299900
  31. 1839,2,349900
  32. 1000,1,169900
  33. 2040,4,314900
  34. 3137,3,579900
  35. 1811,4,285900
  36. 1437,3,249900
  37. 1239,3,229900
  38. 2132,4,345000
  39. 4215,4,549000
  40. 2162,4,287000
  41. 1664,2,368500
  42. 2238,3,329900
  43. 2567,4,314000
  44. 1200,3,299000
  45. 852,2,179900
  46. 1852,4,299900
  47. 1203,3,239500

作者：@臭咸鱼

转载请注明出处：https://www.cnblogs.com/chouxianyu/

欢迎讨论和交流!

sklearn线性回归实现房价预测模型的更多相关文章

  1. 使用sklearn进行数据挖掘-房价预测(5)—训练模型

    使用sklearn进行数据挖掘系列文章: 1.使用sklearn进行数据挖掘-房价预测(1) 2.使用sklearn进行数据挖掘-房价预测(2)-划分测试集 3.使用sklearn进行数据挖掘-房价预 ...

  2. 02-11 RANSAC算法线性回归(波斯顿房价预测)

    目录 RANSAC算法线性回归(波斯顿房价预测) 一.RANSAC算法流程 二.导入模块 三.获取数据 四.训练模型 五.可视化 更新.更全的<机器学习>的更新网站,更有python.go ...

  3. 使用sklearn进行数据挖掘-房价预测(4)—数据预处理

    在使用机器算法之前,我们先把数据做下预处理,先把特征和标签拆分出来 housing = strat_train_set.drop("median_house_value",axis ...

  4. 使用sklearn进行数据挖掘-房价预测(6)—模型调优

    通过上一节的探索,我们会得到几个相对比较满意的模型,本节我们就对模型进行调优 网格搜索 列举出参数组合,直到找到比较满意的参数组合,这是一种调优方法,当然如果手动选择并一一进行实验这是一个十分繁琐的工 ...

  5. 使用sklearn进行数据挖掘-房价预测(1)

    使用sklearn进行数据挖掘系列文章: 1.使用sklearn进行数据挖掘-房价预测(1) 2.使用sklearn进行数据挖掘-房价预测(2)-划分测试集 3.使用sklearn进行数据挖掘-房价预 ...

  6. 使用sklearn进行数据挖掘-房价预测(2)—划分测试集

    使用sklearn进行数据挖掘系列文章: 1.使用sklearn进行数据挖掘-房价预测(1) 2.使用sklearn进行数据挖掘-房价预测(2)-划分测试集 3.使用sklearn进行数据挖掘-房价预 ...

  7. 使用sklearn进行数据挖掘-房价预测(3)—绘制数据的分布

    使用sklearn进行数据挖掘系列文章: 1.使用sklearn进行数据挖掘-房价预测(1) 2.使用sklearn进行数据挖掘-房价预测(2)-划分测试集 3.使用sklearn进行数据挖掘-房价预 ...

  8. Sklearn线性回归

    Sklearn线性回归 原理 线性回归是最为简单而经典的回归模型,用了最小二乘法的思想,用一个n-1维的超平面拟合n维数据 数学形式 \[y(w,x)=w_0+w_1x_1+w_2x_2+-+w_nx ...

  9. 基于sklearn的波士顿房价预测_线性回归学习笔记

    > 以下内容是我在学习https://blog.csdn.net/mingxiaod/article/details/85938251 教程时遇到不懂的问题自己查询并理解的笔记,由于sklear ...

随机推荐

  1. 安装CCS提示错误Windows8.1-KB2999226-x64安装提示 此更新不适用你的计算机

    问题如图所示: 解决方案: 放在D:\目录下 windows键+X  选择  命令提示符(管理员)  一定要是管理员 打开cmd 分别执行下面两句.红色部分就是自己的更新程序了.其他安装同理 例如Wi ...

  2. 第 20 课 go如何实现继承的 && 给引用模块起别名

    golang语言中没有继承,但是可以依靠组合来模拟继承和多态. package controllers import ( "encoding/json" md "gowe ...

  3. Mybatis使用Spring data Pageable的方法

    引言 可能这个用法是个邪教了...但是简单说这都是历史缘故,貌似是项目最初用JPA后面还是换Mybatis了,我接手时候看着那个写好的Controller层觉得换了怪可惜的,就沿用了.网上找找,提供的 ...

  4. 最新 游族网络java校招面经 （含整理过的面试题大全）

    从6月到10月,经过4个月努力和坚持,自己有幸拿到了网易雷火.京东.去哪儿.游族网络等10家互联网公司的校招Offer,因为某些自身原因最终选择了游族网络.6.7月主要是做系统复习.项目复盘.Leet ...

  5. Information Cartography

    作者:Dafna Shahaf 会议:ACM 2015.    研究大背景:自动化地从很大数据集中提取结构化的知识变得越来越难.在本篇文章中,我们将探索我们在文献中(25,26,27)中创立的方法来自 ...

  6. HttpClient的几种请求方式

    public static String doPostToken(String tokenUrl,String clientId,String clientSecret,String grantTyp ...

  7. SQL数据库基础语法

    SQL语句的概述 SQL语言的分类 数据定义语言(Data Definition Language)主要用于修改.创建和删除数据库对象,其中包括CREATE  ALTER  DROP语句. 数据查询语 ...

  8. Java中的静态导入

    Java从1.5开始,增加了静态导入的语法,静态导入使用import static语句,分为两种: 导入指定类的某个静态成员变量.方法. 导入指定类的全部的静态成员变量.方法. 下面是代码演示: /* ...

  9. Vue 组件系统

    vue.js既然是框架,那就不能只是简单的完成数据模板引擎的任务,它还提供了页面布局的功能.本文详细介绍使用vue.js进行页面布局的强大工具,vue.js组件系统. 每一个新技术的诞生,都是为了解决 ...

  10. 【动态规划】Concerts

    Concerts 题目描述 John enjoys listening to several bands, which we shall denote using A through Z. He wa ...