[机器学习] ——KNN K-最邻近算法

KNN分类算法，是理论上比较成熟的方法，也是最简单的机器学习算法之一。

该方法的思路是：如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。

KNN算法中，所选择的邻居都是已经正确分类的对象。该方法在定类决策上只依据最邻近的一个或者几个样本的类别来决定待分样本所属的类别。

一个对于KNN算法解释最清楚的图如下所示：

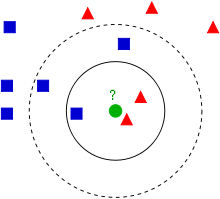
蓝方块和红三角均是已有分类数据，当前的任务是将绿色圆块进行分类判断，判断是属于蓝方块或者红三角。

当然这里的分类还跟K值是有关的：

如果K=3(实线圈)，红三角占比2/3，则判断为红三角；

如果K=5(虚线圈)，蓝方块占比3/5，则判断为蓝方块。

由此可以看出knn算法实际上根本就不用进行训练，而是直接进行计算的，训练时间为0，计算时间为训练集规模n。

knn算法的基本要素大致有3个：

　　1、K 值的选择

　　2、距离的度量

　　3、分类决策规则

---

使用方式：(转载)

1. K 值会对算法的结果产生重大影响。K值较小意味着只有与输入实例较近的训练实例才会对预测结果起作用，容易发生过拟合；如果 K 值较大，优点是可以减少学习的估计误差，缺点是学习的近似误差增大，这时与输入实例较远的训练实例也会对预测起作用，是预测发生错误。在实际应用中，K 值一般选择一个较小的数值，通常采用交叉验证的方法来选择最有的 K 值。随着训练实例数目趋向于无穷和 K=1 时，误差率不会超过贝叶斯误差率的2倍，如果K也趋向于无穷，则误差率趋向于贝叶斯误差率。
2. 算法中的分类决策规则往往是多数表决，即由输入实例的 K 个最临近的训练实例中的多数类决定输入实例的类别
3. 距离度量一般采用 L_p 距离，当p=2时，即为欧氏距离，在度量之前，应该将每个属性的值规范化，这样有助于防止具有较大初始值域的属性比具有较小初始值域的属性的权重过大。

---

knn算法在分类时主要的不足是，当样本不平衡时，如果一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的 K 个邻居中大容量类的样本占多数。

算法伪代码：

 搜索k近邻的算法：kNN(A[n],k)

 #输入：A[n]为N个训练样本在空间中的坐标，k为近邻数
 #输出：x所属的类别

 取A[1]~A[k]作为x的初始近邻，计算与测试样本x间的欧式距离d（x,A[i]）,i=1,2,.....,k；
 按d（x，A[i]）升序排序；
 取最远样本距离D = max{d(x,a[j]) | j=1,2,...,k};

 for(i=k+1;i<=n;i++)#继续计算剩下的n-k个数据的欧氏距离
       计算a[i]与x间的距离d(x,A[i]);
       if(d(x,A[i]))<D
                then 用A[i]代替最远样本#将后面计算的数据直接进行插入即可

  最后的K个数据是有大小顺序的，再进行K个样本的统计即可
  计算前k个样本A[i]),i=1,2,..,k所属类别的概率;
  具有最大概率的类别即为样本x的类

python 函数：

 #knn-k-最临近算法
 #inX为待分类向量，dataSet为训练数据集
 #labels为训练集对应分类，k最邻近算法
 def classify0(inX, dataSet, labels, k):
     dataSetSize = dataSet.shape[0]#获得dataSet的行数

     diffMat = np.tile(inX, (dataSetSize,1)) - dataSet#对应的差值
     sqDiffMat = diffMat**2                           #差的平方
     sqDistances = sqDiffMat.sum(axis=1)              #差的平方的和
     distances = sqDistances**0.5                     #差的平方的和的平方根
     #计算待分类向量与每一个训练数据集的欧氏距离   

     sortedDistIndicies = distances.argsort() #排序后，统计前面K个数据的分类情况

     classCount={}#字典
     for i in range(k):
         voteIlabel = labels[sortedDistIndicies[i]]#labels得是字典才可以如此
         classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1

     sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)#再次排序

     return sortedClassCount[0][0]#第一个就是最多的类别

最后针对于K值的选取，做最后的总结：