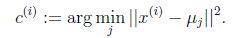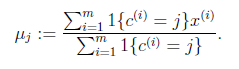R-kmeans聚类算法
K-means也是聚类算法中最简单的一种了,但是里面包含的思想却是不一般。最早我使用并实现这个算法是在学习韩爷爷那本数据挖掘的书中,那本书比较注重应用。看了Andrew Ng的这个讲义后才有些明白K-means后面包含的EM思想。
聚类属于无监督学习,以往的回归、朴素贝叶斯、SVM等都是有类别标签y的,也就是说样例中已经给出了样例的分类。而聚类的样本中却没有给定y,只有特征x,比如假设宇宙中的星星可以表示成三维空间中的点集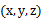 。聚类的目的是找到每个样本x潜在的类别y,并将同类别y的样本x放在一起。比如上面的星星,聚类后结果是一个个星团,星团里面的点相互距离比较近,星团间的星星距离就比较远了。
。聚类的目的是找到每个样本x潜在的类别y,并将同类别y的样本x放在一起。比如上面的星星,聚类后结果是一个个星团,星团里面的点相互距离比较近,星团间的星星距离就比较远了。
在聚类问题中,给我们的训练样本是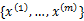 ,每个
,每个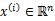 ,没有了y。
,没有了y。
K-means算法是将样本聚类成k个簇(cluster),具体算法描述如下:
|
1、 随机选取k个聚类质心点(cluster centroids)为 2、 重复下面过程直到收敛 { 对于每一个样例i,计算其应该属于的类
对于每一个类j,重新计算该类的质心
} |
K是我们事先给定的聚类数, 代表样例i与k个类中距离最近的那个类,
代表样例i与k个类中距离最近的那个类, 的值是1到k中的一个。质心
的值是1到k中的一个。质心 代表我们对属于同一个类的样本中心点的猜测,拿星团模型来解释就是要将所有的星星聚成k个星团,首先随机选取k个宇宙中的点(或者k个星星)作为k个星团的质心,然后第一步对于每一个星星计算其到k个质心中每一个的距离,然后选取距离最近的那个星团作为
代表我们对属于同一个类的样本中心点的猜测,拿星团模型来解释就是要将所有的星星聚成k个星团,首先随机选取k个宇宙中的点(或者k个星星)作为k个星团的质心,然后第一步对于每一个星星计算其到k个质心中每一个的距离,然后选取距离最近的那个星团作为 ,这样经过第一步每一个星星都有了所属的星团;第二步对于每一个星团,重新计算它的质心
,这样经过第一步每一个星星都有了所属的星团;第二步对于每一个星团,重新计算它的质心 (对里面所有的星星坐标求平均)。重复迭代第一步和第二步直到质心不变或者变化很小。
(对里面所有的星星坐标求平均)。重复迭代第一步和第二步直到质心不变或者变化很小。
下图展示了对n个样本点进行K-means聚类的效果,这里k取2。

K-means面对的第一个问题是如何保证收敛,前面的算法中强调结束条件就是收敛,可以证明的是K-means完全可以保证收敛性。下面我们定性的描述一下收敛性,我们定义畸变函数(distortion function)如下:

J函数表示每个样本点到其质心的距离平方和。K-means是要将J调整到最小。假设当前J没有达到最小值,那么首先可以固定每个类的质心 ,调整每个样例的所属的类别
,调整每个样例的所属的类别 来让J函数减少,同样,固定
来让J函数减少,同样,固定 ,调整每个类的质心
,调整每个类的质心 也可以使J减小。这两个过程就是内循环中使J单调递减的过程。当J递减到最小时,
也可以使J减小。这两个过程就是内循环中使J单调递减的过程。当J递减到最小时, 和c也同时收敛。(在理论上,可以有多组不同的
和c也同时收敛。(在理论上,可以有多组不同的 和c值能够使得J取得最小值,但这种现象实际上很少见)。
和c值能够使得J取得最小值,但这种现象实际上很少见)。
由于畸变函数J是非凸函数,意味着我们不能保证取得的最小值是全局最小值,也就是说k-means对质心初始位置的选取比较感冒,但一般情况下k-means达到的局部最优已经满足需求。但如果你怕陷入局部最优,那么可以选取不同的初始值跑多遍k-means,然后取其中最小的J对应的 和c输出。
和c输出。
下面累述一下K-means与EM的关系,首先回到初始问题,我们目的是将样本分成k个类,其实说白了就是求每个样例x的隐含类别y,然后利用隐含类别将x归类。由于我们事先不知道类别y,那么我们首先可以对每个样例假定一个y吧,但是怎么知道假定的对不对呢?怎么评价假定的好不好呢?我们使用样本的极大似然估计来度量,这里是就是x和y的联合分布P(x,y)了。如果找到的y能够使P(x,y)最大,那么我们找到的y就是样例x的最佳类别了,x顺手就聚类了。但是我们第一次指定的y不一定会让P(x,y)最大,而且P(x,y)还依赖于其他未知参数,当然在给定y的情况下,我们可以调整其他参数让P(x,y)最大。但是调整完参数后,我们发现有更好的y可以指定,那么我们重新指定y,然后再计算P(x,y)最大时的参数,反复迭代直至没有更好的y可以指定。
这个过程有几个难点,第一怎么假定y?是每个样例硬指派一个y还是不同的y有不同的概率,概率如何度量。第二如何估计P(x,y),P(x,y)还可能依赖很多其他参数,如何调整里面的参数让P(x,y)最大。这些问题在以后的篇章里回答。
这里只是指出EM的思想,E步就是估计隐含类别y的期望值,M步调整其他参数使得在给定类别y的情况下,极大似然估计P(x,y)能够达到极大值。然后在其他参数确定的情况下,重新估计y,周而复始,直至收敛。
上面的阐述有点费解,对应于K-means来说就是我们一开始不知道每个样例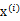 对应隐含变量也就是最佳类别
对应隐含变量也就是最佳类别 。最开始可以随便指定一个
。最开始可以随便指定一个 给它,然后为了让P(x,y)最大(这里是要让J最小),我们求出在给定c情况下,J最小时的
给它,然后为了让P(x,y)最大(这里是要让J最小),我们求出在给定c情况下,J最小时的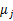 (前面提到的其他未知参数),然而此时发现,可以有更好的
(前面提到的其他未知参数),然而此时发现,可以有更好的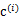 (质心与样例
(质心与样例 距离最小的类别)指定给样例
距离最小的类别)指定给样例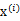 ,那么
,那么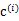 得到重新调整,上述过程就开始重复了,直到没有更好的
得到重新调整,上述过程就开始重复了,直到没有更好的 指定。这样从K-means里我们可以看出它其实就是EM的体现,E步是确定隐含类别变量
指定。这样从K-means里我们可以看出它其实就是EM的体现,E步是确定隐含类别变量 ,M步更新其他参数
,M步更新其他参数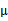 来使J最小化。这里的隐含类别变量指定方法比较特殊,属于硬指定,从k个类别中硬选出一个给样例,而不是对每个类别赋予不同的概率。总体思想还是一个迭代优化过程,有目标函数,也有参数变量,只是多了个隐含变量,确定其他参数估计隐含变量,再确定隐含变量估计其他参数,直至目标函数最优。
来使J最小化。这里的隐含类别变量指定方法比较特殊,属于硬指定,从k个类别中硬选出一个给样例,而不是对每个类别赋予不同的概率。总体思想还是一个迭代优化过程,有目标函数,也有参数变量,只是多了个隐含变量,确定其他参数估计隐含变量,再确定隐含变量估计其他参数,直至目标函数最优。
R-kmeans聚类算法的更多相关文章
- 数据分析与挖掘 - R语言:K-means聚类算法
一个简单的例子!环境:CentOS6.5Hadoop集群.Hive.R.RHive,具体安装及调试方法见博客内文档. 1.分析题目--有一个用户点击数据样本(husercollect)--按用户访问的 ...
- K-Means 聚类算法
K-Means 概念定义: K-Means 是一种基于距离的排他的聚类划分方法. 上面的 K-Means 描述中包含了几个概念: 聚类(Clustering):K-Means 是一种聚类分析(Clus ...
- k-means聚类算法python实现
K-means聚类算法 算法优缺点: 优点:容易实现缺点:可能收敛到局部最小值,在大规模数据集上收敛较慢使用数据类型:数值型数据 算法思想 k-means算法实际上就是通过计算不同样本间的距离来判断他 ...
- 机器学习六--K-means聚类算法
机器学习六--K-means聚类算法 想想常见的分类算法有决策树.Logistic回归.SVM.贝叶斯等.分类作为一种监督学习方法,要求必须事先明确知道各个类别的信息,并且断言所有待分类项都有一个类别 ...
- 一步步教你轻松学K-means聚类算法
一步步教你轻松学K-means聚类算法(白宁超 2018年9月13日09:10:33) 导读:k-均值算法(英文:k-means clustering),属于比较常用的算法之一,文本首先介绍聚类的理 ...
- K-means聚类算法原理和C++实现
给定训练集$\{x^{(1)},...,x^{(m)}\}$,想把这些样本分成不同的子集,即聚类,$x^{(i)}\in\mathbb{R^{n}}$,但是这是个无标签数据集,也就是说我们再聚类的时候 ...
- K-means聚类算法(转)
K-means聚类算法 想想常见的分类算法有决策树.Logistic回归.SVM.贝叶斯等.分类作为一种监督学习方法,要求必须事先明确知道各个类别的信息,并且断言所有待分类项都有一个类别与之对应.但是 ...
- Hadoop平台K-Means聚类算法分布式实现+MapReduce通俗讲解
Hadoop平台K-Means聚类算法分布式实现+MapReduce通俗讲解 在Hadoop分布式环境下实现K-Means聚类算法的伪代码如下: 输入:参数0--存储样本数据的文本文件inpu ...
- 03-01 K-Means聚类算法
目录 K-Means聚类算法 一.K-Means聚类算法学习目标 二.K-Means聚类算法详解 2.1 K-Means聚类算法原理 2.2 K-Means聚类算法和KNN 三.传统的K-Means聚 ...
- K-Means 聚类算法原理分析与代码实现
前言 在前面的文章中,涉及到的机器学习算法均为监督学习算法. 所谓监督学习,就是有训练过程的学习.再确切点,就是有 "分类标签集" 的学习. 现在开始,将进入到非监督学习领域.从经 ...
随机推荐
- getOutputStream() has already been called for this response
错误日志里偶尔会有getOutputStream() has already been called for this response这个错误 最近发现了高概率复现条件,所以顺手解决了一下: 首先根 ...
- Linux 更改ssh 端口
部署了一个测试服务器之后,在查看linux日志的时候,发现莫名的IP一直在访问服务器,感觉像是某种恶意扫描,来攻击服务器的.因此更改ssh端口. 输入: vim /etc/ssh/sshd_confi ...
- postman安装使用教程---图文讲解
一.安装postman 1,安装包安装 官网下载地址:https://www.getpostman.com 选择好对应的版本下载,下载完后直接安装 2,插件包安装 可以在谷歌的应用商店里面找到,或者在 ...
- [AHOI2004]奇怪的字符串
[AHOI2004]奇怪的字符串 题目描述 输入输出格式 输入格式: 输入文件中包含两个字符串X和Y.当中两字符串非0即1.序列长度均小于9999. 输出格式: X和Y的最长公共子序列长度. 输入输出 ...
- C++Builder中MessageBox的基本用法
C++Builder中MessageBox的基本用法 返回值:IDYES=Application->MessageBox("","",MBYESNO) i ...
- CentOS 引导 Win10 启动项
因为无聊,所以想尝试一下双系统,所以在win10的基础之上,装了一个Linux系统,之前装过Ubuntu,几乎都是自动完成的无任何压力.但是想着Ubuntu好像更新换代有点快,所以换了个能用比较久的C ...
- 关于如何更好地使用Github的一些建议
关于如何更好地使用Github的一些建议 原文(Github repository形式): https://github.com/Wasdns/github-example-repo 本文记录了我对于 ...
- hdu1878判断欧拉回路
欧拉回路 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submi ...
- Ubuntu Docker 版本的更新与安装
突然发现自己的docker 版本特别的低,目前是1.9.1 属于古董级别的了,想更新一下最新版本,这样最新的一下命令就可以被支持.研究了半天都没有更新成功,更新后的版本始终都是1.9.1 :蒙圈了,找 ...
- 22.Linux-块设备驱动之框架详细分析(详解)
本节目的: 通过分析块设备驱动的框架,知道如何来写驱动 1.之前我们学的都是字符设备驱动,先来回忆一下 字符设备驱动: 当我们的应用层读写(read()/write())字符设备驱动时,是按字节/字符 ...

 。
。