POJ 3398 Perfect Service（树型动态规划，最小支配集）

Description

A network is composed of N computers connected by N − 1 communication links such that any two computers can be communicated via a unique route. Two computers are said to be adjacent if there is a communication link between them. The neighbors of a computer is the set of computers which are adjacent to it. In order to quickly access and retrieve large amounts of information, we need to select some computers acting as servers to provide resources to their neighbors. Note that a server can serve all its neighbors. A set of servers in the network forms a perfect service if every client (non-server) is served by exactly one server. The problem is to find a minimum number of servers which forms a perfect service, and we call this number perfect service number.

We assume that N (≤ 10000) is a positive integer and these N computers are numbered from 1 to N. For example, Figure 1 illustrates a network comprised of six computers, where black nodes represent servers and white nodes represent clients. In Figure 1(a), servers 3 and 5 do not form a perfect service because client 4 is adjacent to both servers 3 and 5 and thus it is served by two servers which contradicts the assumption. Conversely, servers 3 and 4 form a perfect service as shown in Figure 1(b). This set also has the minimum cardinality. Therefore, the perfect service number of this example equals two.

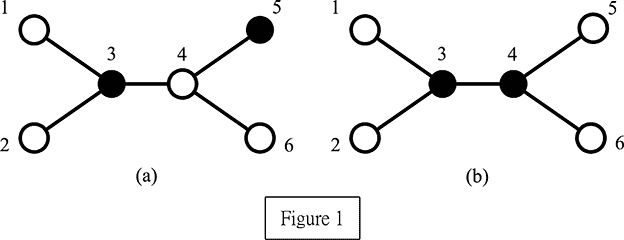
Your task is to write a program to compute the perfect service number.

Input

The input consists of a number of test cases. The format of each test case is as follows: The first line contains one positive integer, N, which represents the number of computers in the network. The next N − 1 lines contain all of the communication links and one line for each link. Each line is represented by two positive integers separated by a single space. Finally, a 0 at the (N + 1)th line indicates the end of the first test case.

The next test case starts after the previous ending symbol 0. A −1 indicates the end of the whole inputs.

Output

The output contains one line for each test case. Each line contains a positive integer, which is

the perfect service number.

Sample Input

6

1 3

2 3

3 4

4 5

4 6

0

2

1 2

-1

Sample Output

2

1

Http

POJ:https://vjudge.net/problem/POJ-3398

Source

树型动态规划，最小支配集

题目大意

在一棵n个点的树中求一个最小的点集，使得该树上的点满足在这个子集中或与子集中的点相邻，另外，不在该点集中的还满足有且仅与一个在点集中的点相邻。

解决思路

这道题的解决方法与POJ3659差不多，基本的思路可以参照我以前写的文章

那么这道题不同的地方就是非服务器不能连接到多台服务器，所以我们的动态转移方程就要改一改。

（这里先假设读者已经阅读了笔者在上面给出的文章，本文中的各变量意义与上文中的一致）

首先，关于F[u][0]的改变。因为F[u][0]代表是把u作为服务器的情况，所以在本题中它不能由F[v][1]推导得，因为F[v][1]表示v被v的子节点覆盖，若由被u覆盖，与题意相悖。

第二，F[u][2]数组不能从F[v][2]推导得，同样也是上面的原因

第三，F[u][1]现在有且只能被一个子节点覆盖，所以笔者把F[u][1]的计算方式改变了一下（具体方式请看代码，非常巧妙哦！）

代码

#include<iostream>

#include<cstdio>

#include<cstdlib>

#include<cstring>

#include<algorithm>

#include<vector>

using namespace std;

const int maxN=10001;

const int inf=147483647;

int n;

int cnt;

vector<int> E[maxN];

bool vis[maxN];

int F[maxN][5];

void dfs(int u);

int main()

{

    while (cin>>n)

    {

        if (n==-1)

            break;

        for (int i=1;i<=n;i++)

            E[i].clear();

        for (int i=1;i<n;i++)

        {

            int x,y;

            cin>>x>>y;

            E[x].push_back(y);

            E[y].push_back(x);

        }

        int A;

        cin>>A;

        memset(vis,0,sizeof(vis));

        memset(F,0,sizeof(vis));

        dfs(1);

        cout<<min(F[1][1],F[1][0])<<endl;

        if (A==-1)

            break;

    }

    return 0;

}

void dfs(int u)

{

    vis[u]=1;

    F[u][0]=1;

    F[u][2]=0;

    F[u][1]=inf;

    for (int i=0;i<E[u].size();i++)

    {

        int v=E[u][i];

        if (vis[v]==0)

        {

            dfs(v);

            F[u][0]+=min(F[v][0],F[v][2]);

            F[u][2]+=F[v][1];

            F[u][1]=min(F[u][1],F[v][0]-F[v][1]);//巧妙之处在这里，这样就可以保证除了选出的F[v][0]-F[v][1]最小的v是从F[v][0]得到

        }

    }

    F[u][1]+=F[u][2];//还有这里，最后加上所有的F[v][1]之和

    return;

}