[Luogu P2014]选课 (树形DP)

题面

传送门：https://www.luogu.org/problemnew/show/P2014

---

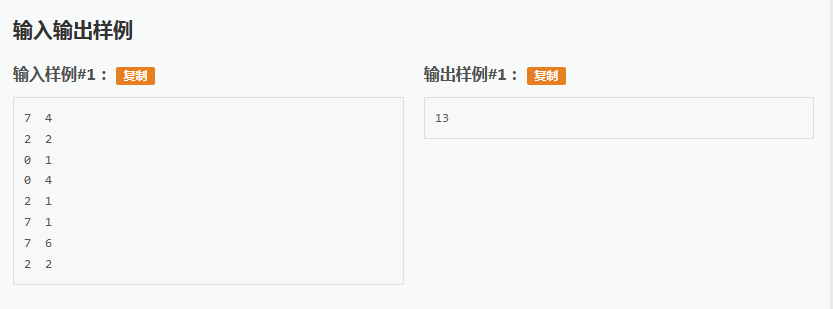
Solution

这是一道十分经典的树形DP题，这种类型的树形DP有一种很普遍的解法。

首先，观察题目，我们把这道题转换一下：给定一颗树，选出包含1号节点（根)的一颗子树，使得点权和最大。

我们可以这样子定义状态：

设f[i][j] 表示以i为根节点的子树，选出j个节点，所能达到的最大点权值。

对于二叉树来说，转移很显然，就是枚举左子树分配多少个节点，就可以对应的得出右子树能分配到多少个节点，对所有情况取最大值就好。

对于多叉树来说，问题就没有那么简单了，这里，我们有两个方案可以解决这个问题：

一是多叉树转二叉树，

二是树上背包。

因为我不会多叉树转二叉树，所以在这里我主要讲一讲第二种方法。

我们一般在树上做的是多重背包问题。

我以本题为例子，讲一下树上如何做多重背包。

首先，我们肯定要一层循环枚举子树(可以类似为背包问题中枚举第几件物品)。

第二层循环我们得枚举当前以节点的子树能分配的节点数（可以类似为背包问题中枚举背包容量）

*这一层循环一定要从后往前枚举，类似与背包压在一维做的做法*

第三层循环我们就可以枚举当前子树分配多少个节点了（可以类似多重背包中枚举第i件物品要几件）

下面是这种枚举在这道题应用的代码：

1     for(int i=0;i<int(e[x].size());i++)//枚举子树
2     {
3         int temp=dfs(e[x][i]);//先把子树的f递归下去算出来
4         tot+=temp;//tot记录到当前子树为止总节点数
5         for(int j=tot;j>=1;j--)//枚举自己这颗树的总分配数
6             for(int k=0;k<=temp;k++)//枚举子树分配多少个节点
7                 if(j-k>=1)
8                     f[x][j]=max(f[x][j],f[x][j-k]+f[e[x][i]][k]);
9     }

树上背包一般看上去是三重循环，非常恐怖。

但事实上，根据一堆证明（不会证），其复杂度为两重循环。

所以复杂度应该是O（能过）

复杂度是O(N*N*M)

---

Code

树上背包有成吨的细节，建议参考代码

#include<iostream>
#include<cstdio>
#include<vector>
using namespace std;
long long read()
{
    long long x=0,f=1;char c=getchar();
    while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}
const int N=300+10;
vector <int> e[N];
long long n,m,f[N][N],v[N];
int dfs(int x)
{
    int tot=1;
    f[x][1]=v[x];
    for(int i=0;i<int(e[x].size());i++)
    {
        int temp=dfs(e[x][i]);
        tot+=temp;
        for(int j=tot;j>=1;j--)
            for(int k=0;k<=temp;k++)
                if(j-k>=1)
                    f[x][j]=max(f[x][j],f[x][j-k]+f[e[x][i]][k]);
    }
    return tot;
}
int main()
{
    n=read(),m=read();
    for(int i=0;i<=n;i++)
        e[i].reserve(4);
    for(int i=1;i<=n;i++)
    {
        e[read()].push_back(i);
        v[i]=read();
    }

    dfs(0);

    printf("%lld",f[0][m+1]);
    return 0;
}

正解(c++)