霍夫曼编码(Huffman)

题目：有一个字符串：cabcedeacacdeddaaaba，问题：

（1）采用霍夫曼编码画出编码的过程，并写出各字符的编码

（2）根据求得的编码，求得各编码需要的总位数

（3）求出整个字符串总编码长度，并计算出字符串位数在编码前与编码后的比值

解答：
（1）各字符出现频率统计如下表所示。

符号	出现次数	出现频率
a	7	0.35
b	2	0.1
c	4	0.2
d	4	0.2
e	3	0.15

编码过程如下图所示：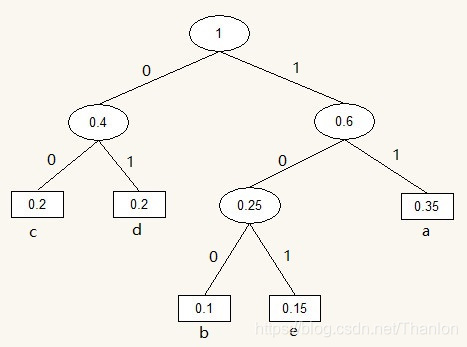

各字符编码如下表所示：

符号	编码（码字）
a	11
b	100
c	00
d	01
e	101

（2）由（1）可进一步知道字符编码的码长和需要的位数

符号	符号出现次数	概率	编码（码字）	码长	需要的位数
a	7	0.35	11	2	14
b	2	0.1	100	3	6
c	4	0.2	00	2	8
d	4	0.2	01	2	8
e	3	0.15	101	3	9

根据求得的编码，求得各编码需要的总位数是：45位（14+6+8+8+9=45）。
（3）字符串总编码长度：60bit（20 x 3 = 60)。
编码前与编码后的比值：4/3（编码前是60，编码后是45）