POJ2074 Line of Sight

嘟嘟嘟




题意：用一条水平线段表示以栋房子：\((x_0, y_0)(x_0', y_0)\)。然后有一条低于房子的水平线段\(l_0\)，代表你可以到的位置。接下来输入一个数\(n\)，一下\(n\)行每行\(3\)个数，用一条水平线段代表障碍物。求你在\(l_0\)上能看到房子的最大连续长度。（看到房子指房子完全没被挡上）




刚开始自己\(yy\)了一个\(O(n ^ 2)\)的算法，结果\(TLE\)了……谁叫这题不告诉我数据范围的。

正解比较有意思：我们要逆向思维：对于一个障碍物，求出它能遮挡的范围，那么最后的答案就是没被遮挡的区间长度的最大值。

遮挡的范围画个图就明白了：



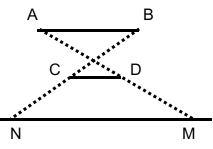
则\([N, M]\)就是被遮挡的区间，然后用叉积求交点即可。

那么现在我们就得到了一堆区间（可能重叠），然后想括号匹配一样跑一边，如果当前栈空，就那\(a _ {i + 1} - a _ i\)更新答案。

需要注意的是\([N, M]\)可能在直线\(l_0\)之外，这时候那\(l_0\)两个端点限制\(N, M\)即可，具体看代码。

还有一点就是区间的头和尾的地方要单独算一下，即\(a _ 1 - L\)和\(R - a _ n\)

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<cstdlib>
#include<cctype>
#include<vector>
#include<stack>
#include<queue>
using namespace std;
#define enter puts("")
#define space putchar(' ')
#define Mem(a, x) memset(a, x, sizeof(a))
#define rg register
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-8;
const int maxn = 5e4 + 5;
inline ll read()
{
  ll ans = 0;
  char ch = getchar(), last = ' ';
  while(!isdigit(ch)) last = ch, ch = getchar();
  while(isdigit(ch)) ans = (ans << 1) + (ans << 3) + ch - '0', ch = getchar();
  if(last == '-') ans = -ans;
  return ans;
}
inline void write(ll x)
{
  if(x < 0) x = -x, putchar('-');
  if(x >= 10) write(x / 10);
  putchar(x % 10 + '0');
}
int n;
struct Vec
{
  db x, y;
  db operator * (const Vec& oth)const
  {
    return x * oth.y - oth.x * y;
  }
};
struct Point
{
  db x, y;
  Vec operator - (const Point& oth)const
  {
    return (Vec){x - oth.x, y - oth.y};
  }
}H1, H2, L1, L2;
struct Node
{
  db x; int flg;
  bool operator < (const Node& oth)const
  {
    return x < oth.x;
  }
}a[maxn];
int cnt = 0;
void solve(Point A, Point B, int flg)
{
  Vec AB = B - A;
  Vec CA = A - L1, CD = L2 - L1, DB = B - L2;
  db s1 = CA * CD, s2 = -(DB * CD);
  db ret = A.x + AB.x / (s1 + s2) * s1;
  if(ret > L2.x) ret = L2.x;  //限制N, M
  if(ret < L1.x) ret = L1.x;
  a[++cnt] = (Node){ret, flg};
}
int main()
{
  while(scanf("%lf%lf%lf", &H1.x, &H2.x, &H1.y))
    {
      if(H1.x == 0 && H1.y == 0 && H2.x == 0) break;
      cnt = 0;
      H2.y = H1.y;
      scanf("%lf%lf%lf", &L1.x, &L2.x, &L1.y); L2.y = L1.y;
      n = read();
      for(int i = 1; i <= n; ++i)
	{
	  db L, R, y;
	  scanf("%lf%lf%lf", &L, &R, &y);
	  if(y < L1.y || y >= H1.y) continue;
	  solve(H1, (Point){R, y}, -1);
	  solve(H2, (Point){L, y}, 1);
	}
      if(!n) {printf("%.2f\n", L2.x - L1.x); continue;}
      sort(a + 1, a + cnt + 1);
      a[cnt + 1].x = L2.x;
      db ans = max(0.00, a[1].x - L1.x);
      int st = 0;  //模仿栈操作
      for(int i = 1; i <= cnt; ++i)
	{
	  st += a[i].flg;
	  if(!st) ans = max(ans, a[i + 1].x - a[i].x);
	}
      if(ans == 0) puts("No View");
      else printf("%.2f\n", ans);
    }
  return 0;
}