一步一步详解ID3和C4.5的C++实现

1. 关于ID3和C4.5的原理介绍这里不赘述，网上到处都是，可以下载讲义c9641_c001.pdf或者参考李航的《统计学习方法》.

2. 数据与数据处理

• 本文采用下面的训练数据：

• 数据处理：本文只采用了"Outlook", "Humidity", "Windy"三个属性，然后根据Humidity的值是否大于75，将Humidity的值归为两类，Play Golf 的值就是类别标签，只有yes 和 no两类
• 训练集是字符和数字的混合，这会给编程带来麻烦，所以首先把训练集用数字表示出来：

   const unsigned att_num = ;
   const unsigned rule_num = ;
   string decision_tree_name("Play Golf ?");
   string attribute_names[] = {"Outlook", "Humidity", "Windy"};
   string attribute_values[] = {"Sunny", "Overcast", "Rainy", "> 75", "<= 75", "True", "False", "Yes", "No"};
   //训练集最后一列为分类标签，所以总列数为属性数加1
   unsigned train_data[rule_num][att_num + ] = {
                       {, , , },{, , , },{, , , },
                       {, , , },{, , , },{, , , },
                       {, , , },{, , , },{, , , },
                       {, , , },{, , , },{, , , },
                       {, , , },{, , , }
                                   };

  以train_data的第一行{0, 3, 6, 8}为例解释：前三列值对应的属性与attribute_names中的元素分别对应，最后一列是类别标签的值，0 表示 attribute_values的第1个元素，即”Sunny“，类似3便是attribute_values的第4个元素"> 75"，6 是 "False"，8 是"No"，所以{0, 3, 6, 8} 代表的实例就是:

　　  

　　  其他实例都是以这样的方式数字化，方便编程.

3. 编写必要函数

因为ID3和C4.5都需要计算属性的信息增益，C4.5还需要计算属性的信息增益比，所正确编写这两个函数很重要，对比着讲义c9641_c001.pdf或者其他参考资料，编写出这两个函数.(代码最后附上)

4. 确定数据结构

这是最重要的一环，明确目的：构造一个决策树！这就直接决定了编程的正确或者难易，网上有很多例子，但是我觉得不够简洁，这里我采用一种简单且容易理解的方式：

 struct Tree{
     unsigned root;//节点属性值
     vector<unsigned> branches;//节点可能取值
     vector<Tree> children; //孩子节点
 };

每一个决策树都是由根节点开始，然后有很多分支，分支连接着孩子节点，而每一个孩子节点以及这个孩子节点对应的所有子孙又可以组成一棵树，这是一个不断递归的过程，所以采用了上面的数据结构.

5. 构造决策树

有了上面的基础，开始着手构造决策树,根据规则选出某一属性作为根节点，根据根节点的取值确定分支，然后构造孩子节点，根据上面的陈述可以知道，每一个孩子节点及其后面的子孙又是一棵树，所以这是一个递归操作，即采用前面同样的方式来构造这个子树，以此类推。

6. 打印决策树

因为树的结构是递归的，所以打印决策树同样是一个递归的过程。

7. 代码实现

 /*************************************************
 Copyright:1.0
 Author:90Zeng
 Date:2014-11-25
 Description:ID3/C4.5 algorithm
 **************************************************/
 
 #include <iostream>
 #include <cmath>
 #include <vector>
 #include <string>
 #include <algorithm>
 using namespace std;
 
 const unsigned att_num = ;
 const unsigned rule_num = ;
 string decision_tree_name("Play Golf ?");
 string attribute_names[] = {"Outlook", "Humidity", "Windy"};
 string attribute_values[] = {"Sunny", "Overcast", "Rainy", "> 75", "<= 75", "True", "False", "Yes", "No"};
 //训练集最后一列为分类标签，所以总列数为属性数加1
 unsigned train_data[rule_num][att_num + ] = {
                     {, , , },{, , , },{, , , },
                     {, , , },{, , , },{, , , },
                     {, , , },{, , , },{, , , },
                     {, , , },{, , , },{, , , },
                     {, , , },{, , , }
                                 };
 
 /*************************************************
 Function:       unique()
 Description:    将vector中重复元素合并，只保留一个
 Calls:          无
 Input:          vector
 Output:         vector
 *************************************************/
 template <typename T>
 vector<T> unique(vector<T> vals)
 {
     vector<T> unique_vals;
     vector<T>::iterator itr;
     vector<T>::iterator subitr;
 
     int flag = ;
     while( !vals.empty() )
     {
         unique_vals.push_back(vals[]);
         itr = vals.begin();
         subitr = unique_vals.begin() + flag;
         while ( itr != vals.end())
         {
             if (*subitr == *itr)
                 itr = vals.erase(itr);
             else
                 itr++;
         }
         flag++;
     }
     return unique_vals;
 }
 
 /*************************************************
 Function:       log2()
 Description:    计算一个数值得以2为底的对数
 Calls:          无
 Input:          double
 Output:         double
 *************************************************/
 
 double log2(double n)
 {
     return log10(n) / log10(2.0);
 }
 
 /*************************************************
 Function:       compute_entropy()
 Description:    根据属性的取值，计算该属性的熵
 Calls:          unique(),log2(),count(),其中count()
                 在STL的algorithm库中
 Input:          vector<unsigned>
 Output:         double
 *************************************************/
 double compute_entropy(vector<unsigned> v)
 {
     vector<unsigned> unique_v;
     unique_v = unique(v);
 
     vector<unsigned>::iterator itr;
     itr = unique_v.begin();
 
     double entropy = 0.0;
     auto total = v.size();
     while(itr != unique_v.end())
     {
         double cnt = count(v.begin(), v.end(), *itr);
         entropy -= cnt / total * log2(cnt / total);
         itr++;
     }
     return entropy;
 }
 
 /*************************************************
 Function:       compute_gain()
 Description:    计算数据集中所有属性的信息增益
 Calls:          compute_entropy(),unique()
 Input:          vector<vector<unsigned> >
                 相当于一个二维数组，存储着训练数据集
 Output:         vector<double> 存储着所有属性的信息
                 增益
 *************************************************/
 vector<double> compute_gain(vector<vector<unsigned> > truths)
 {
     vector<double> gain(truths[].size() - , );
     vector<unsigned> attribute_vals;
     vector<unsigned> labels;
     for(unsigned j = ; j < truths.size(); j++)
     {
         labels.push_back(truths[j].back());
     }
 
     for(unsigned i = ; i < truths[].size() - ; i++)//最后一列是类别标签，没必要计算信息增益
     {
         for(unsigned j = ; j < truths.size(); j++)
         attribute_vals.push_back(truths[j][i]);
 
         vector<unsigned> unique_vals = unique(attribute_vals);
         vector<unsigned>::iterator itr = unique_vals.begin();
         vector<unsigned> subset;
         while(itr != unique_vals.end())
         {
             for(unsigned k = ; k < truths.size(); k++)
             {
                 if (*itr == attribute_vals[k])
                 {
                     subset.push_back(truths[k].back());
                 }
             }
             double A = (double)subset.size();
             gain[i] += A / truths.size() * compute_entropy(subset);
             itr++;
             subset.clear();
         }
         gain[i] = compute_entropy(labels) - gain[i];
         attribute_vals.clear();
     }
     return gain;
 }
 
 /*************************************************
 Function:       compute_gain_ratio()
 Description:    计算数据集中所有属性的信息增益比
                 C4.5算法中用到
 Calls:          compute_gain();compute_entropy()
 Input:          训练数据集
 Output:         信息增益比
 *************************************************/
 vector<double> compute_gain_ratio(vector<vector<unsigned> > truths)
 {
     vector<double> gain = compute_gain(truths);
     vector<double> entropies;
     vector<double> gain_ratio;
 
     for(unsigned i = ; i < truths[].size() - ; i++)//最后一列是类别标签，没必要计算信息增益比
     {
         vector<unsigned> attribute_vals(truths.size(), );
         for(unsigned j = ; j < truths.size(); j++)
         {
             attribute_vals[j] = truths[j][i];
         }
         double current_entropy = compute_entropy(attribute_vals);
         if (current_entropy)
         {
             gain_ratio.push_back(gain[i] / current_entropy);
         }
         else
             gain_ratio.push_back(0.0);
 
     }
     return gain_ratio;
 }
 
 /*************************************************
 Function:       find_most_common_label()
 Description:    找出数据集中最多的类别标签
 
 Calls:          count();
 Input:          数据集
 Output:         类别标签
 *************************************************/
 template <typename T>
 T find_most_common_label(vector<vector<T> > data)
 {
     vector<T> labels;
     for (unsigned i = ; i < data.size(); i++)
     {
         labels.push_back(data[i].back());
     }
     vector<T>:: iterator itr = labels.begin();
     T most_common_label;
     unsigned most_counter = ;
     while (itr != labels.end())
     {
         unsigned current_counter = count(labels.begin(), labels.end(), *itr);
         if (current_counter > most_counter)
         {
             most_common_label = *itr;
             most_counter = current_counter;
         }
         itr++;
     }
     return most_common_label;
 }
 
 /*************************************************
 Function:       find_attribute_values()
 Description:    根据属性，找出该属性可能的取值
 
 Calls:          unique();
 Input:          属性，数据集
 Output:         属性所有可能的取值(不重复)
 *************************************************/
 template <typename T>
 vector<T> find_attribute_values(T attribute, vector<vector<T> > data)
 {
     vector<T> values;
     for (unsigned i = ; i < data.size(); i++)
     {
         values.push_back(data[i][attribute]);
     }
     return unique(values);
 }
 
 /*************************************************
 Function:       drop_one_attribute()
 Description:    在构建决策树的过程中，如果某一属性已经考察过了
                 那么就从数据集中去掉这一属性，此处不是真正意义
                 上的去掉，而是将考虑过的属性全部标记为110，当
                 然可以是其他数字，只要能和原来训练集中的任意数
                 字区别开来即可
 Calls:          unique();
 Input:          属性，数据集
 Output:         属性所有可能的取值(不重复)
 *************************************************/
 template <typename T>
 vector<vector<T> > drop_one_attribute(T attribute, vector<vector<T> > data)
 {
     vector<vector<T> > new_data(data.size(),vector<T>(data[].size() - , ));
     for (unsigned i = ; i < data.size(); i++)
     {
         data[i][attribute] = ;
     }
     return data;
 }
 
 struct Tree{
     unsigned root;//节点属性值
     vector<unsigned> branches;//节点可能取值
     vector<Tree> children; //孩子节点
 };
 
 /*************************************************
 Function:       build_decision_tree()
 Description:    递归构建决策树
 
 Calls:          unique()，count(),
                 find_most_common_label()
                 compute_gain()(ID3),
                 compute_gain_ratio()(C4.5),
                 find_attribute_values(),
                 drop_one_attribute(),
                 build_decision_tree()(递归，
                 当然要调用函数本身)
 Input:          训练数据集，一个空决策树
 Output:         无
 *************************************************/
 void build_decision_tree(vector<vector<unsigned> > examples, Tree &tree)
 {
     //第一步：判断所有实例是否都属于同一类，如果是，则决策树是单节点
     vector<unsigned> labels(examples.size(), );
     for (unsigned i = ; i < examples.size(); i++)
     {
         labels[i] = examples[i].back();
     }
     if (unique(labels).size() == )
     {
         tree.root = labels[];
         return;
     }
 
     //第二步：判断是否还有剩余的属性没有考虑，如果所有属性都已经考虑过了，
     //那么此时属性数量为0，将训练集中最多的类别标记作为该节点的类别标记
     if (count(examples[].begin(),examples[].end(),) == examples[].size() - )//只剩下一列类别标记
     {
         tree.root = find_most_common_label(examples);
         return;
     }
     //第三步:在上面两步的条件都判断失败后，计算信息增益，选择信息增益最大
     //的属性作为根节点,并找出该节点的所有取值
 
     vector<double> standard = compute_gain(examples);
 
     //要是采用C4.5，将上面一行注释掉，把下面一行的注释去掉即可
     //vector<double> standard = compute_gain_ratio(examples);
     tree.root = ;
     for (unsigned i = ; i < standard.size(); i++)
     {
         if (standard[i] >= standard[tree.root] && examples[][i] != )
             tree.root  = i;
     }
 
     tree.branches = find_attribute_values(tree.root, examples);
     //第四步:根据节点的取值，将examples分成若干子集
     vector<vector<unsigned> > new_examples = drop_one_attribute(tree.root, examples);
     vector<vector<unsigned> > subset;
     for (unsigned i = ; i < tree.branches.size(); i++)
     {
         for (unsigned j = ; j < examples.size(); j++)
         {
             for (unsigned k = ; k < examples[].size(); k++)
             {
                 if (tree.branches[i] == examples[j][k])
                     subset.push_back(new_examples[j]);
             }
         }
         // 第五步:对每一个子集递归调用build_decision_tree()函数
         Tree new_tree;
         build_decision_tree(subset,new_tree);
         tree.children.push_back(new_tree);
         subset.clear();
     }
 }
 
 /*************************************************
 Function:       print_tree()
 Description:    从第根节点开始，逐层将决策树输出到终
                 端显示
 
 Calls:          print_tree();
 Input:          决策树，层数
 Output:         无
 *************************************************/
 void print_tree(Tree tree,unsigned depth)
 {
     for (unsigned d = ; d < depth; d++) cout << "\t";
     if (!tree.branches.empty()) //不是叶子节点
     {
         cout << attribute_names[tree.root] << endl;
 
         for (unsigned i = ; i < tree.branches.size(); i++)
         {
             for (unsigned d = ; d < depth + ; d++) cout << "\t";
             cout << attribute_values[tree.branches[i]] << endl;
             print_tree(tree.children[i],depth + );
         }
     }
     else //是叶子节点
     {
         cout << attribute_values[tree.root] << endl;
     }
 
 }
 
 int main()
 {
     vector<vector<unsigned> > rules(rule_num, vector<unsigned>(att_num + , ));
     for(unsigned i = ; i < rule_num; i++)
     {
         for(unsigned j = ; j <= att_num; j++)
             rules[i][j] = train_data[i][j];
     }
     Tree tree;
     build_decision_tree(rules, tree);
     cout << decision_tree_name << endl;
     print_tree(tree,);
     return ;
 }

8.运行结果：

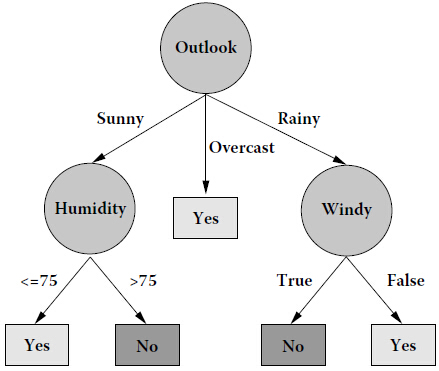
前者是采用ID3运行的结果，后者是讲义c9641_c001.pdf给出的构造的决策树，二者一致，验证了程序的正确性.

9.总结

所谓”百鸟在林，不如一鸟在手“, ID3和C4.5的思想都很简单，容易理解，但是在实现的的过程中由于数据结构的确定和递归调用等问题，还是调试了很久，收获很多，实践出真知！