4923: [Lydsy1706月赛]K小值查询 平衡树 非旋转Treap

国际惯例的题面: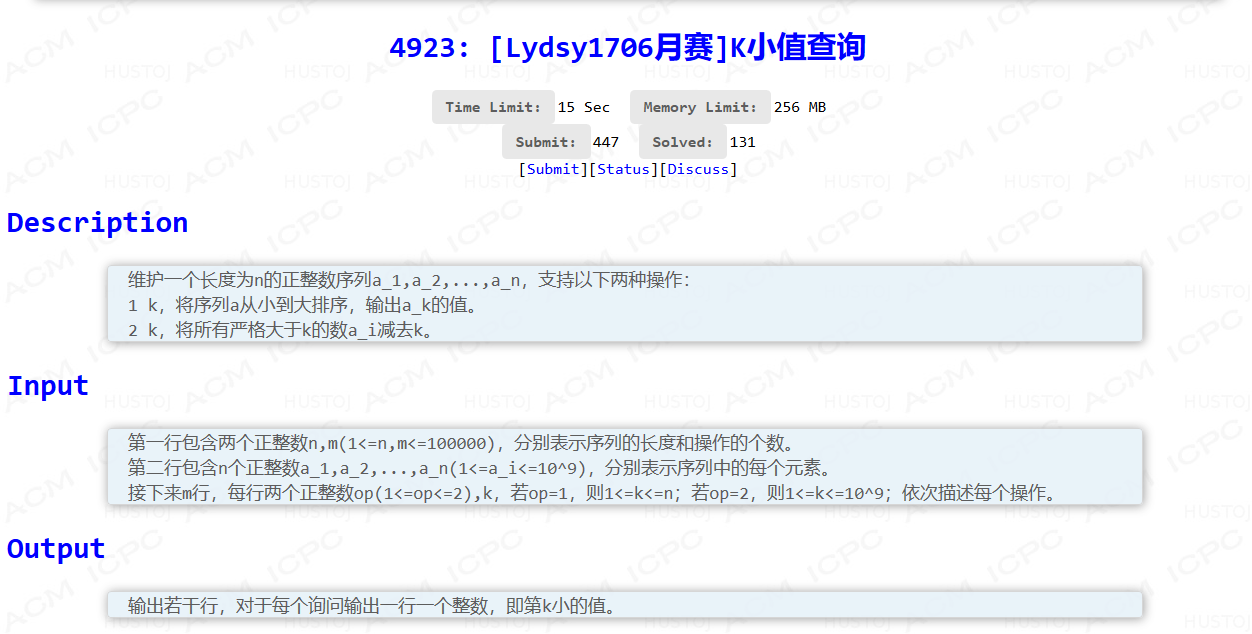

这种维护排序序列，严格大于的进行操作的题都很套路......
我们按照[0,k],(k,2k],(2k,inf)分类讨论一下就好。
显然第一个区间的不会变化，第二个区间的会被平移进第一个区间，第三个区间的相对大小不会变化。
于是我们直接把第二个区间拆了重构，一个一个插入第一个区间即可。因为每次这样做最少减半，所以每个元素只会被重构log次，复杂度nlog^2n。
这种按照值域分离区间的操作，非旋转treap实现起来是最简单的......
然而第一次写非旋转treap还是出了一点问题，注意它的插入是通过按照值域分裂，新建点，再进行两次合并实现的。直接插入复杂度不对。
另外区间值域存在重合的情况两个treap不能直接合并......
我写的判定size的版本复杂度好像不对(不如暴力快？)，于是只好预先生成fix值。

代码:

 #include<cstdio>
 #include<algorithm>
 #include<cstdlib>
 const int maxn=1e5+1e2;

 typedef std::pair<int,int> pii;
 __inline pii mp(const int &x,const int &y) { return std::make_pair(x,y); }

 int seq[maxn],sql;
 int stk[maxn],top;

 struct Treap {
     int lson[maxn],rson[maxn],lazy[maxn],val[maxn],siz[maxn],fix[maxn],cnt;

     inline void init(int n) {
         for(int i=;i<=n;i++) fix[i] = i;
         std::random_shuffle(fix+,fix++n);
     }
     inline void apply(int pos,int x) {
         if(pos) lazy[pos] += x , val[pos] -= x;
     }
     inline void push(int pos) {
         if( lazy[pos] ) apply(lson[pos],lazy[pos]) , apply(rson[pos],lazy[pos]) , lazy[pos] = ;
     }
     inline void maintain(int pos) {
         siz[pos] = siz[lson[pos]] + siz[rson[pos]] + ;
     }

     inline pii split(int pos,int dv) { // left is <= , right is > .
         if( !pos ) return mp(,);
         push(pos);
         if(  dv < val[pos] ) {
             pii spl = split(lson[pos],dv);
             lson[pos] = spl.second , maintain(pos);
             return mp(spl.first,pos);
         } else {
             pii spr = split(rson[pos],dv);
             rson[pos] = spr.first , maintain(pos);
             return mp(pos,spr.second);
         }
     }
     inline int merge(int x,int y) {
         if( !x || !y ) return x | y;
         push(x) , push(y);
         if( val[x] > val[y] ) std::swap(x,y);
         if( fix[x] > fix[y] ) { // siz[x] is bigger .
             lson[y] = merge(lson[y],x) , maintain(y);
             return y;
         } else {
             rson[x] = merge(rson[x],y) , maintain(x);
             return x;
         }
     }
     inline void dfs(int pos) {
         if( !pos ) return;
         seq[++sql] = val[pos] , push(pos);
         dfs(lson[pos]) , dfs(rson[pos]);
         lson[pos] = rson[pos] = siz[pos] =  , stk[++top] = pos;
     }
     inline int kth(int pos,int k) { // return the kth value .
         if( k == siz[lson[pos]] +  ) return val[pos];
         return push(pos) , k <= siz[lson[pos]] ? kth(lson[pos],k) : kth(rson[pos],k-siz[lson[pos]]-);
     }
     inline void insert(int &root,int x) {
         val[++cnt] = x , siz[cnt] = ;
         pii sp = split(root,x);
         root = merge(sp.first,cnt) , root = merge(root,sp.second);
     }
     inline void reinsert(int &root,int x) {
         int cur = stk[top--];
         val[cur] = x , siz[cur] = ;
         pii sp = split(root,x);
         root = merge(sp.first,cur) , root = merge(root,sp.second);
     }

 }tp;

 int main() {
     static int n,m,root,rtl,rtm,rtr;
     scanf("%d%d",&n,&m) , tp.init(n);
     for(int i=,t;i<=n;i++) scanf("%d",&t) , tp.insert(root,t);
     for(int i=,o,x;i<=m;i++) {
         scanf("%d%d",&o,&x);
         if( o ==  ) printf("%d\n",tp.kth(root,x));
         else if( o ==  ) {
             pii sp = tp.split(root,x);
             rtl = sp.first , sp = tp.split(sp.second,x<<);
             rtm = sp.first , rtr = sp.second;
             sql =  , tp.dfs(rtm) , tp.apply(rtr,x);
             for(int i=;i<=sql;i++) tp.reinsert(rtl,seq[i]-x);
             root = tp.merge(rtl,rtr);
         }
     }
     return ;
 }

Thupc被拒了好气啊！我们队可是有yzy大爷的！(即使这样都被拒了，一看就是我太菜了)

ありのままでいればいつも
只要坚守自我维持现状
あるべき私かここにいると
自己希望成为的样貌就存在于此
信じてまた 新しい夢を
不要放弃希望 崭新的梦想
精一杯描き出せばいい
再次奋力地去描绘就好
そう気づき始めたよ私
是啊 而我开始意识到
みんなとただ笑ってる未来を
大家单纯地绽放笑容的未来
夢見て
诚心盼望