【极角排序、扫描线】UVa 1606 - Amphiphilic Carbon Molecules（两亲性分子）

Shanghai Hypercomputers, the world's largest computer chip manufacturer, has invented a new class of nanoparticles called Amphiphilic Carbon Molecules (ACMs). ACMs are semiconductors. It means that they can be either conductors or insulators of electrons, and thus possess a property that is very important for the computer chip industry. They are also amphiphilic molecules, which means parts of them are hydrophilic while other parts of them are hydrophobic. Hydrophilic ACMs are soluble in polar solvents (for example, water) but are insoluble in nonpolar solvents (for example, acetone). Hydrophobic ACMs, on the contrary, are soluble in acetone but insoluble in water. Semiconductor ACMs dissolved in either water or acetone can be used in the computer chip manufacturing process.

As a materials engineer at Shanghai Hypercomputers, your job is to prepare ACM solutions from ACM particles. You go to your factory everyday at 8 am and find a batch of ACM particles on your workbench. You prepare the ACM solutions by dripping some water, as well as some acetone, into those particles and watch the ACMs dissolve in the solvents. You always want to prepare unmixed solutions, so you first separate the ACM particles by placing an Insulating Carbon Partition Card (ICPC) perpendicular to your workbench. The ICPC is long enough to completely separate the particles. You then drip water on one side of the ICPC and acetone on the other side. The ICPC helps you obtain hydrophilic ACMs dissolved in water on one side and hydrophobic ACMs dissolved in acetone on the other side. If you happen to put the ICPC on top of some ACM particles, those ACMs will be right at the border between the water solution and the acetone solution, and they will be dissolved. Fig.1 shows your working situation.

Fig.1

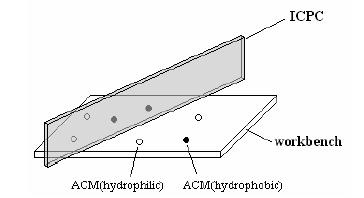
Your daily job is very easy and boring, so your supervisor makes it a little bit more challenging by asking you to dissolve as much ACMs into solution as possible. You know you have to be very careful about where to put the ICPC since hydrophilic ACMs on the acetone side, or hydrophobic ACMs on the water side, will not dissolve. As an experienced engineer, you also know that sometimes it can be very difficult to find the best position for the ICPC, so you decide to write a program to help you. You have asked your supervisor to buy a special digital camera and have it installed above your workbench, so that your program can obtain the exact positions and species (hydrophilic or hydrophobic) of each ACM particle in a 2D pictures taken by the camera. The ICPC you put on your workbench will appear as a line in the 2D pictures.

Fig.2

Input

There will be no more than 10 test cases. Each case starts with a line containing an integer N, which is the number of ACM particles in the test case. N lines then follow. Each line contains three integers x, y, r, where (x, y) is the position of the ACM particle in the 2D picture and r can be 0 or 1, standing for the hydrophilic or hydrophobic type ACM respectively. The absolute value of x, y will be no larger than 10000. You may assume that N is no more than 1000. N = 0 signifies the end of the input and need not be processed. Fig.2 shows the positions of ACM particles and the best ICPC position for the last test case in the sample input.

Output

For each test case, output a line containing a single integer, which is the maximum number of dissolved ACM particles.

Sample Input

3
0 0 0
0 1 0
2 2 1
4
0 0 0
0 4 0
4 0 0
1 2 1
7
-1 0 0
1 2 1
2 3 0
2 1 1
0 3 1
1 4 0
-1 2 0
0

【题意】　　给定平面上的n个点，分别为黑色和白色，现在需要放置一条隔板，使得隔板一侧的白点数目加上另一侧的黑点总数最大。隔板上的点可以看做是在任意一侧；

【分析】　　贪心策略：假设隔板一定经过至少两个点；

　　　　　　方法:①暴力枚举--先枚举两个点，然后输出两侧黑白点的个数。复杂度O(n^3).90%会TLE...；
　　　　　　　　 ②先找一个基准点，让隔板绕该点旋转。每当隔板扫过一个点就动态修改两侧的点数。在此之前，需对所有点相对于基准点（即将基准点看做（0,0））进行极角排序。复杂度O(n^2*logn);
【NOTE】　　极角排序:通俗的说，就是根据坐标系内每一个点与x轴所成的角，逆时针比较，。按照角度从小到大的方式排序。用到的函数是atan2(y, x);
　　　　　　 扫描线：这个概念也比较好理解。注意动态维护的时候细节问题（代码中会有详解，当然只针对自己这种第一次接触看不懂人家代码的菜）。
　　　　　 　小技巧：因题目要求求两侧不同颜色的点数和，可以预处理将黑点做中心对称。这样原本位于两侧的黑白点的点就会分布在同一侧内了（真心巧妙。。。）；
【代码】

 #include<iostream>
 #include<cstdio>
 #include<cstdlib>
 #include<cmath>
 #include<algorithm>
 using namespace std;
 const int maxn = ;
 struct Node
 {
     int x, y;
     double rad;
     int col;
     bool operator < (const Node& a) const
     {
         return rad < a.rad;
     }
 }node[maxn], tnode[maxn];
 int Cross(Node a, Node b)
 {
     return (a.x*b.y - b.x*a.y) >= ;
 }
 int main()
 {
     //freopen("out.txt", "w", stdout) ;
     int n, ans, cnt = ;
     while(scanf("%d", &n) && n)
     {
         ans = ;
         for(int i = ; i < n; i++)
         {
             scanf("%d%d%d", &node[i].x, &node[i].y, &node[i].col);
         }
         if(n <= ) {printf("%d\n", n); continue;}
         cnt = ;
         for(int basicp = ; basicp < n; basicp++) //基准点
         {
             for(int i = ; i < n; i++) //各点相对于基准点的坐标
             {
                 if(i == basicp) continue;
                 tnode[cnt].x = node[i].x-node[basicp].x;
                 tnode[cnt].y = node[i].y-node[basicp].y;
                 if(node[i].col) {tnode[cnt].x = -tnode[cnt].x; tnode[cnt].y = -tnode[cnt].y;} //对黑点中心对称
                 tnode[cnt].rad = atan2(tnode[cnt].y, tnode[cnt].x); //求极角
                 cnt++;
             }
             sort(tnode, tnode+cnt); //极角排序。几何意义为由x轴正半轴逆时针旋转；
             int l = , r = ; //l, r:求tnode[l~r]之间的点
             int sum = ; //注意这个sum = 2;
             while(l < cnt)
             {
                 if(r == l) //主要针对初始情况
                 {
                     r=(r+)%cnt;  sum++;
                 }
                 while(l != r&&Cross(tnode[l],tnode[r])) //Cross(tnode[l],tnode[r]) 叉积:若小于0则两点的夹角大于180度。跳出循环
                 {
                     r=(r+)%cnt;  sum++;
                 }
                 sum--;  //sum-1主要是为了在枚举新的起点时减去老的起点。而初始sum=2也是为了符合这一条件
                 l++; //枚举新的起点
                 ans=max(ans,sum);
             }
         }
         cout << ans << endl;
     }
     return ;
 }

【总结】　　看代码很明显又是看了别人的。希望能长个教训吧，以后遇到类似的题自己能独立写出来、