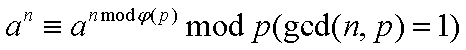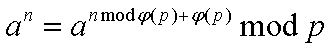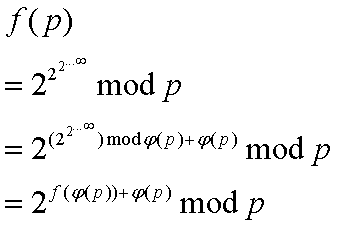P4139 上帝与集合的正确用法
本题是欧拉定理的应用。我这种蒟蒻当然不知道怎么证明啦!
那么我们就不证明了,来直接看结论:

或者
ab≡⎧⎩⎨⎪⎪ab%ϕ(p) gcd(a,p)=1ab gcd(a,p)≠1,b<ϕ(p)ab%ϕ(p)+ϕ(p) gcd(a,p)≠1,b≥ϕ(p) (mod pab≡⎧⎩⎨⎪⎪ab%ϕ(p) gcd(a,p)=1ab gcd(a,p)≠1,b<ϕ(p)ab%ϕ(p)+ϕ(p) gcd(a,p)≠1,b≥ϕ(p) (mod p)
或者观看这个
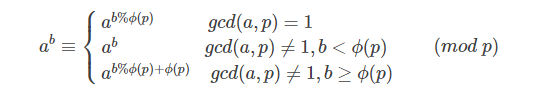
那么再来看本题,主要使用了后者:
所以可以写出递归式:
f(p)=qpow(2,f(ask_phi(p))+ask_phi(p),p);
得解。
题外话:我本来先打个表求出10^7以内的phi[],然后直接调用的,结果全T...
发现n<=1000,就用了ask_phi(),然后就过了。
#include <cstdio>
using namespace std;
const int N = ;
typedef long long LL; LL phi[N]; void make_phi(int n)
{
for(int i=;i<=n;i++) phi[i]=i;
for(int i=;i<=n;i+=) phi[i]/=;
for(int i=;i<=n;i+=)
{
if(phi[i]==i)
{
for(int j=i;j<=n;j+=i) phi[j]=(phi[j]/i)*(i-);
}
}
return;
} LL ask_phi(int x)
{
LL ans=x;
for(int i=;i*i<=x;i++)
{
if(x%i==)
{
while(x%i==) x/=i;
ans=(ans/i)*(i-);
}
}
if(x>) ans=(ans/x)*(x-);
return ans;
} LL qpow(LL a,LL b,LL m)
{
LL ans=;
while(b)
{
if(b&) ans=(ans*a)%m;
b=b>>;
a=(a*a)%m;
}
return ans;
} LL f(int p)
{
if(p==) return ;
return qpow(,f(ask_phi(p))+ask_phi(p),p);
} int main()
{
int n,x;
scanf("%d",&n);
//make_phi(N);
while(n--)
{
scanf("%d",&x);
printf("%lld\n",f(x));
}
return ;
}
AC代码
我们学到了什么姿势:
1.欧拉函数:φ(n)=[1,n]中与n互质的数的个数。
求phi(x):
LL ask_phi(int x)
{
LL ans=x;
for(int i=;i*i<=x;i++)
{
if(x%i==)
{
while(x%i==) x/=i;
ans=(ans/i)*(i-);
}
}
if(x>) ans=(ans/x)*(x-);
return ans;
}
ask_phi()
打表phi[]:
void make_phi(int n)
{
for(int i=;i<=n;i++) phi[i]=i;
for(int i=;i<=n;i+=) phi[i]/=;
for(int i=;i<=n;i+=)
{
if(phi[i]==i)
{
for(int j=i;j<=n;j+=i) phi[j]=(phi[j]/i)*(i-);
}
}
return;
}
make_phi()
二进制快速幂:
LL qpow(LL a,LL b,LL m)
{
LL ans=;
while(b)
{
if(b&) ans=(ans*a)%m;
b=b>>;
a=(a*a)%m;
}
return ans;
}
qpow()
P4139 上帝与集合的正确用法的更多相关文章
- 洛谷 P4139 上帝与集合的正确用法 解题报告
P4139 上帝与集合的正确用法 题目描述 根据一些书上的记载,上帝的一次失败的创世经历是这样的: 第一天, 上帝创造了一个世界的基本元素,称做"元". 第二天, 上帝创造了一个新 ...
- 洛谷P4139 上帝与集合的正确用法 [扩展欧拉定理]
题目传送门 上帝与集合的正确用法 题目描述 根据一些书上的记载,上帝的一次失败的创世经历是这样的: 第一天, 上帝创造了一个世界的基本元素,称做“元”. 第二天, 上帝创造了一个新的元素,称作“α”. ...
- 题解-洛谷P4139 上帝与集合的正确用法
上帝与集合的正确用法 \(T\) 组数据,每次给定 \(p\),求 \[\left(2^{\left(2^{\left(2^{\cdots}\right)}\right)}\right)\bmod p ...
- 洛谷 P4139 上帝与集合的正确用法
题目描述 根据一些书上的记载,上帝的一次失败的创世经历是这样的: 第一天, 上帝创造了一个世界的基本元素,称做“元”. 第二天, 上帝创造了一个新的元素,称作“α”.“α”被定义为“元”构成的集合.容 ...
- 【洛谷】P4139 上帝与集合的正确用法
题目描述 根据一些书上的记载,上帝的一次失败的创世经历是这样的: 第一天,上帝创造了一个世界的基本元素,称做“元”. 第二天,上帝创造了一个新的元素,称作“α”.“α”被定义为“元”构成的集合.容 ...
- 洛谷P4139 上帝与集合的正确用法 拓欧
正解:拓展欧拉定理 解题报告: 首先放上拓欧公式? if ( b ≥ φ(p) ) ab ≡ ab%φ(p)+φ(p)(mod p)else ab≡ab mod φ(p) (mod p) 首先利用扩 ...
- [洛谷P4139]上帝与集合的正确用法
题目大意:多次询问,每次给你$p$询问$2^{2^{2^{\dots}}}\bmod p$ 题解:扩展欧拉定理,求出$\varphi(p)$即可.因为$2^{2^{2^{\dots}}}>> ...
- Luogu P4139 上帝与集合的正确用法【扩展欧拉定理】By cellur925
题目传送门 题目中的式子很符合扩展欧拉定理的样子.(如果你还不知扩展欧拉定理,戳).对于那一堆糟心的2,我们只需要递归即可,递归边界是模数为1. 另外,本题中好像必须要用快速乘的样子...否则无法通过 ...
- luogu P4139 上帝与集合的正确用法(扩展欧拉定理)
本蒟蒻现在才知带扩展欧拉定理. 对于任意的\(b\geq\varphi(p)\)有 \(a^b\equiv a^{b\ mod\ \varphi(p)+\varphi(p)}(mod\ p)\) 当\ ...
随机推荐
- http指南(2)--代理
代理 单个客户端专用的代理称为私有代理,众多客户端共享的代理被称为公共代理 代理与网关的对比:代理连接的是两个或多个使用相同协议的应用程序,而网关连接的则是两个或多个使用不同协议的端点.网关扮演的是“ ...
- .NETCore_初探
1. Core默认的服务注册 Statup文件(rogram类型中创建 WebHost时使用的)中有俩个方法: Configure和ConfigureServices(将服务放置到容器里面) publ ...
- MySQL的启动程序
1.mysqld: mysql server [root@test bin]# ./mysqld --user=mysql & [root@test bin]# ps ...
- Notes of Daily Scrum Meeting(12.23)
今天的团队任务总结如下: 团队成员 今日团队工作 陈少杰 调试网络连接,寻找新的连接方法 王迪 建立搜索的UI界面 金鑫 查阅相关资料,熟悉后台的接口 雷元勇 建立搜索的界面 高孟烨 继续美化界面,熟 ...
- zookeeper安装Linux
安装环境: Linux:centos6.4 Jdk:1.7以上版本 Zookeeper是java开发的可以运行在windows.linux环境.需要先安装jdk. 安装步骤: 第一步:安装jdk 第二 ...
- JavaScript的类、对象、原型、继承、引用
以CSS为例,有一种为所有class为"xxxx"的元素添加样式(外联样式),那么所有class为xxx的元素样式就会改变,在css中像下面这么写: <html> &l ...
- JDK学习AbstractQueuedSynchronizer和AbstractQueuedLongSynchronizer
AbstractQueuedLongSynchronizer类是扩展自AbstractQueuedSynchronizer的,实现了java.io.Serializable接口. 其中提到的wait ...
- Robot Framework 入门教程总结
Robot Framework 作为一款通用测试框架,可加载多种测试库.驱动多种测试工具,并可对各种自定义脚本进行集成.对于Robot Framework,我准备将其分为 入门--Robot Fram ...
- [Wiki].NET框架
.NET框架 建议将.NET Framework 3.0并入本条目或章节.(讨论) .NET框架 .NET框架的组件堆栈 开发者 Microsoft 初始版本 2002年2月13日,16年前 稳定 ...
- 浅谈cpu.idle和cpu.load
1.概述 大家经常对一个系统的容量进行评估时,会参考cpu.idle和cpu.load指标,但是这两个指标到底在什么区间,表示系统是正常或者异常呢,业内有不同的说法.因此本文搜集一些资料,并对一个系统 ...