N数码问题的启发式搜索算法--A*算法python实现

• 一、启发式搜索：A算法

1）评价函数的一般形式 : f(n) = g(n) + h(n)

g(n):从S0到Sn的实际代价(搜索的横向因子)

h(n):从N到目标节点的估计代价,称为启发函数(搜索的纵向因子);

特点: 效率高, 无回溯,

搜索算法

OPEN表 : 存放待扩展的节点.

CLOSED表 : 存放已被扩展过的节点.

2）评价函数  f(x) = g(x) + h(x)

当f(x) = g(x)   时，为宽度优先搜索

当f(x) = 1/g(x)时，为深度优先搜索

当f(x) = h(x)   时，为全局优先搜索

比较f(x)大小，决定节点搜索顺序，即在OPEN表中的顺序

3)Step1:   把初始节点S0放入OPEN表中;

Step2:   若OPEN表为空,则搜索失败,退出.

Step3:   移出OPEN中第一个节点N放入CLOSED表中, 并标以顺序号n;

Step4:   若目标节点Sg=N, 则搜索成功,结束.

Step5:   若N不可扩展, 则转Step2;

Step6:   扩展N, 生成一组子节点, 对这组子节点作如下处理后, 放入  OPEN表, 按f值重新排序OPEN表, 转 Step2;

删除重复节点和修改返回指针处理.

• 二、启发式搜索：A*算法

1）评价函数的一般形式:

f(n) = g(n) + h(n)  且  h(n) <= h*(n)

g(n),h(n):定义同A算法;

h*(n):从N到目标节点的最短路径; 称此时的A算法为A*算法.

2）程序关键点

节点的扩展：close表存放已经扩展后的状态，open表存放未扩展的状态。首先获取节点能扩展的方向，扩展后将父节点放入close表中，如果转移之后的节点，既不在close表也不再open表，表明该节点还未被扩展，则插入open表，如果在close表中表明之前已经扩展过该状态，为了避免无限扩展应将该状态从open表舍弃，如果在open表则比较这两个矩阵的f值（选取最优解），留小的在open表，之后对open表中的节点根据f值进行排序，pop出f值最小的节点进行扩展，依次进行该过程，直至该节点为目标状态。
解的路径的输出：通过目标状态节点向上回溯找其父节点，直至开始状态。

• 三、python代码实现

 # -*- coding: utf-8 -*-
 """
 Created on Sun Sep 16 14:31:40 2018
 A*算法解决N数码问题
 运行程序后如下是输入格式:
         请输入矩阵的行数

         3                            输入对应的N
         请输入初始矩阵A               

         1 0 2                        一行行输入，每行数字空格隔开，每行最后一个数字输入完成后直接回车开始输入第二行

         4 5 6

         3 7 8
         请输入目标矩阵B

         1 2 3

         8 0 4

         7 6 5

 """
 import numpy as np
 import copy
 import time
 from operator import itemgetter

 goal = {}

 def get_location(vec, num):    #根据num元素获取num在矩阵中的位置
     row_num = vec.shape[0]     #numpy-shape函数获得矩阵的维数
     line_num = vec.shape[1]

     for i in range(row_num):
         for j in range(line_num):
             if num == vec[i][j]:
                 return i, j

 def get_actions(vec):    #获取当前位置可以移动的下一个位置，返回移动列表
     row_num = vec.shape[0]
     line_num = vec.shape[1]

     (x, y) = get_location(vec, 0)    #获取0元素的位置
     action = [(0, 1), (0, -1), (1, 0), (-1, 0)]

     if x == 0:    #如果0在边缘则依据位置情况，减少0的可移动位置
         action.remove((-1, 0))
     if y == 0:
         action.remove((0, -1))
     if x == row_num - 1:
         action.remove((1, 0))
     if y == line_num - 1:
         action.remove((0, 1))

     return list(action)

 def result(vec, action):    #移动元素，进行矩阵转化
      (x, y) = get_location(vec, 0)    #获取0元素的位置
      (a, b) = action    #获取可移动位置

      n = vec[x+a][y+b]    #位置移动，交换元素
      s = copy.deepcopy(vec)
      s[x+a][y+b] = 0
      s[x][y] = n

      return s

 def get_ManhattanDis(vec1, vec2):    #计算两个矩阵的曼哈顿距离,vec1为目标矩阵,vec2为当前矩阵
     row_num = vec1.shape[0]
     line_num = vec1.shape[1]
     dis  = 0

     for i in range(row_num):
         for j in range(line_num):
             if vec1[i][j] != vec2[i][j] and vec2[i][j] != 0:
                 k, m = get_location(vec1, vec2[i][j])
                 d = abs(i - k) + abs(j - m)
                 dis += d

     return dis

 def expand(p, actions, step):                          #actions为当前矩阵的可扩展状态列表,p为当前矩阵,step为已走的步数
     children = []                                      #children用来保存当前状态的扩展节点
     for action in actions:
         child = {}
         child['parent'] = p
         child['vec'] = (result(p['vec'], action))
         child['dis'] = get_ManhattanDis(goal['vec'], child['vec'])
         child['step'] = step + 1                       #每扩展一次当前已走距离加1
         child['dis'] = child['dis'] + child['step']    #更新该节点的f值  f=g+h（step+child[dis]）
         child['action'] = get_actions(child['vec'])
         children.append(child)

     return children

 def node_sort(nodelist):    #按照节点中字典的距离字段对列表进行排序,从大到小
     return sorted(nodelist, key = itemgetter('dis'), reverse=True)

 def get_input(num):
     A = []
     for i in range(num):
         temp = []
         p = []
         s = input()
         temp = s.split(' ')
         for t in temp:
             t = int(t)
             p.append(t)
         A.append(p)

     return A  

 def get_parent(node):
     q = {}
     q = node['parent']
     return q

 def test():
     openlist = []    #open表
     close = []       #存储扩展的父节点

     print('请输入矩阵的行数')
     num = int(input())  

     print("请输入初始矩阵A")
     A = get_input(num)

     print("请输入目标矩阵B")
     B = get_input(num)

     print("请输入结果文件名")
     resultfile = input()

     goal['vec'] = np.array(B)   #建立矩阵

     p = {}
     p['vec'] = np.array(A)
     p['dis'] = get_ManhattanDis(goal['vec'], p['vec'])
     p['step'] = 0
     p['action'] = get_actions(p['vec'])
     p['parent'] = {}

     if (p['vec'] == goal['vec']).all():
         return

     openlist.append(p)

     start_CPU = time.clock()    #开始扩展时CPU开始计算

     while openlist:

         children = []

         node = openlist.pop()    #node为字典类型，pop出open表的最后一个元素
         close.append(node)  #将该元素放入close表

         if (node['vec'] == goal['vec']).all():    #比较当前矩阵和目标矩阵是否相同
             end_CPU = time.clock()    #CPU结束计算

             h = open(resultfile,'w',encoding='utf-8',)  #将结果写入文件  并在控制台输出
             h.write('搜索树规模：' + str(len(openlist)+len(close)) + '\n')
             h.write('close：' + str(len(close)) + '\n')
             h.write('openlist：' + str(len(openlist)) + '\n')
             h.write('cpu运行时间：' + str(end_CPU - start_CPU) + '\n')
             h.write('路径长：' + str(node['dis']) + '\n')

             h.write('解的路径：' + '\n')
             i = 0
             way = []
             while close:
                 way.append(node['vec'])  #从最终状态开始依次向上回溯将其父节点存入way列表中
                 node = get_parent(node)
                 if(node['vec'] == p['vec']).all():
                     way.append(node['vec'])
                     break
             while way:
                 i += 1
                 h.write(str(i) + '\n')
                 h.write(str(way.pop()) + '\n')
             h.close()
             f = open(resultfile,'r',encoding='utf-8',)
             print(f.read())

             return

         children = expand(node, node['action'], node['step'])    #如果不是目标矩阵，对当前节点进行扩展，取矩阵的可能转移情况

         for child in children:     #如果转移之后的节点，既不在close表也不再open表则插入open表，如果在close表中则舍弃，如果在open表则比较这两个矩阵的f值，留小的在open表
             f = False
             flag = False
             j = 0
             for i in range(len(openlist)):
                 if (child['vec'] == openlist[i]['vec']).all():
                     j = i
                     flag = True
                     break
             for i in range(len(close)):
                 if(child['vec'] == close[i]).all():
                     f = True
                     break
             if  f == False and flag == False :
                 openlist.append(child)

             elif flag == True:
                 if child['dis'] < openlist[j]['dis']:
                     del openlist[j]
                     openlist.append(child)

         openlist = node_sort(openlist)   #对open表进行从大到小排序

 test()

• 四、程序运行结果如下图所示

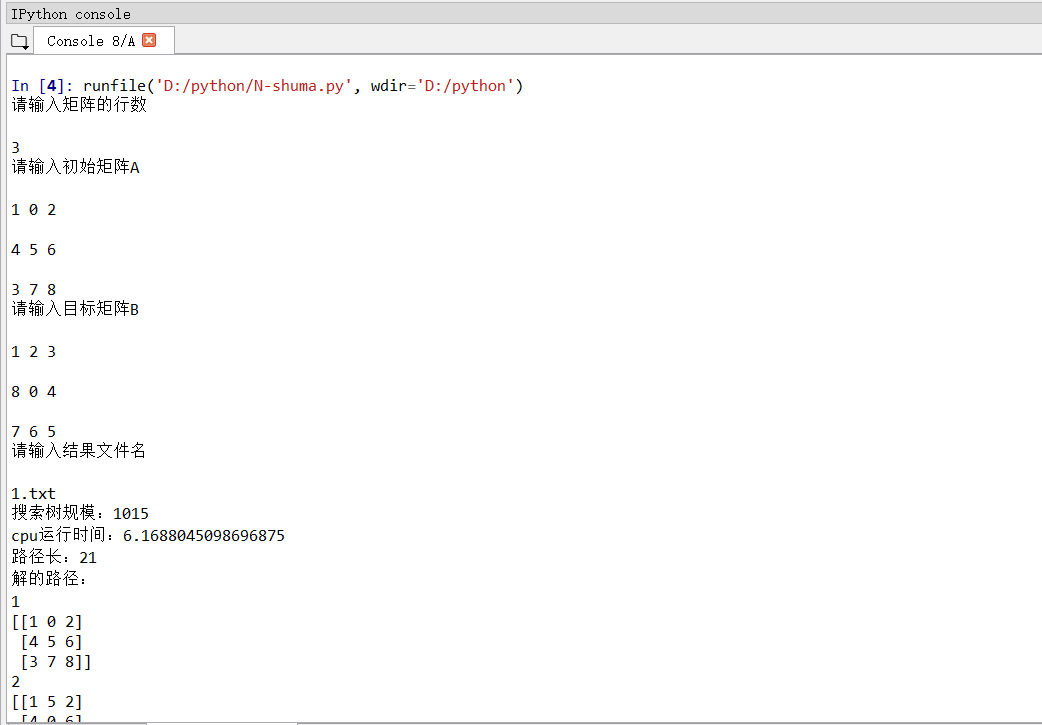
图 1

 

图 2

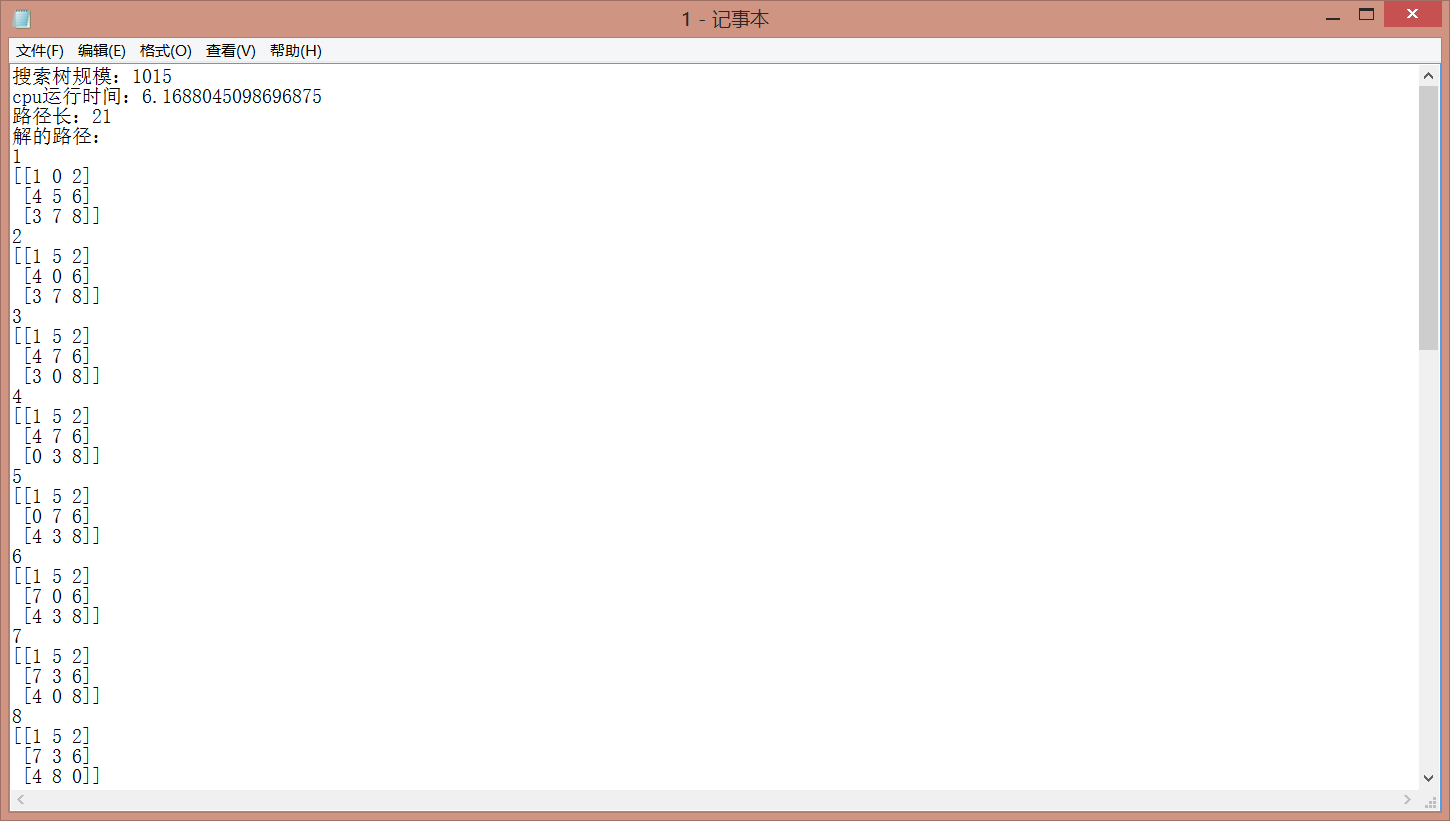
图 3

• 五、总结

通过这次编程了解到了搜索具有探索性，要提高搜索效率(尽快地找到目标节点)，或要找最佳路径(最佳解)就必须注意搜索策略。对于状态图搜索，已经提出了许多策略，它们大体可分为盲目搜索（bland search)和启发式搜索（heuristic search）两大类。其中盲目搜索是无向导搜索。启发式搜索是有向导搜索，即利用启发信息（函数）引导去寻找问题解。通过A*算法解决N数码问题实验过程中也遇到很多问题，比如节点扩展的方向问题等，通过这次实验不仅锻炼了自己python编程能力，也让自己对N数码求解最优路径问题有了更清晰的认识，希望自己能在老师和同学的帮助下，能不断进步，当然最重要的是自己得付出，只会幻想而不行动的人,永远也体会不到收获果实时的喜悦。加油！！