每一个each（Power Query 之 M 语言）

each _

固定结构，表示每一个（废话，each这单词中文意思就是每一个）

但后面的下划线，是个省略参数的写法……

首先，each后面不是非要跟_

其次，_代表的意思是指定列里同行的每一个，这时的公式中已经有指定列

第三，_和指定列不能随意互换

第四，each和_之间有空格

第五，each和_之间可以有“第三者”

第六，each不一定是一个值，也可以是table、list等，就看表中指定列里是什么内容。

对比以下三个M公式

= Table.AddColumn(步骤名, "新列名", each [已有列名]+100)

= Table.TransformColumns(步骤名, {"已有列名", each _ +100})

= Table.TransformColumns(步骤名, {"已有列名", each 100+_})

第一个公式，在已有列的基础上加上新的一列，并在原基础上加100。

第二个公式，将已有列转换成新的内容，结果是原有列加100，_指“已有列名”中同行的每一个值。

第三个公式，同上。

以上，支持头晕模式！

好吧，说人话：

数据源：

某列数据，标题名“已有列名”

公式1：

= Table.AddColumn(步骤名, "新列名", each [已有列名]+100)

效果1：

　　

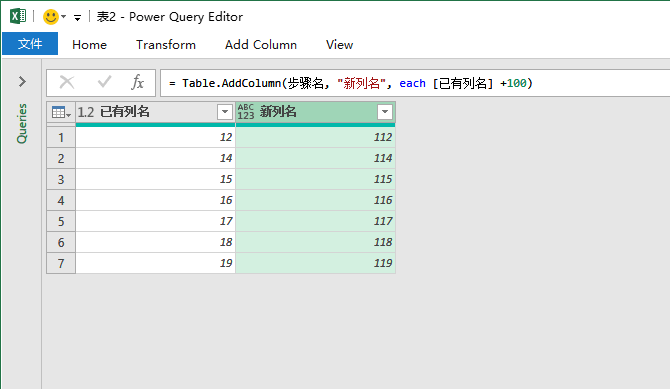
公式2：

= Table.TransformColumns(步骤名, {"已有列名", each _ +100})

效果2：

　　

公式3：

= Table.TransformColumns(步骤名, {"已有列名", each 100+_})

效果3：