[Luogu P3986] 斐波那契数列 (逆元)

题面

传送门：https://www.luogu.org/problemnew/show/P3986

---

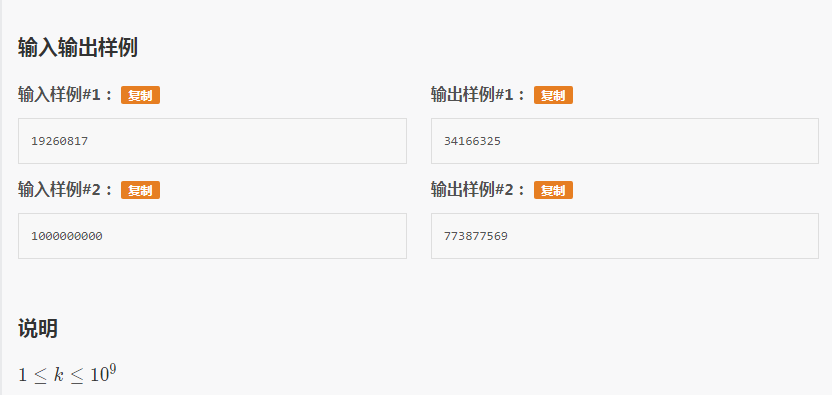
Solution

这是一道很有意思的数论题。

首先，我们可以发现直接枚举a和b会T的起飞。

接下来，我们就可以观察一下式子了，我们略微手算一下，就会有这样的结果：

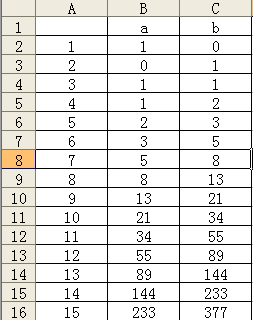
我们可以发现，a，b在每一项中的数量都可以用同一个斐波那契数列表示。

我们可以用g[x]表示斐波那契数列的第x项，那么，我们可以得到f[x]=a*g[x-1]+b*g[x]

接下来，由常识可以知道，斐波那契数列的第40项就差不多有10^9那么大了。

所以说，我们可以考虑枚举当前项x，问题就变为了有多少个a，b使得 K=a*g[x-1]+b*g[x]

移项得：b=(K-g[x-1]*a)/g[x]

因为a，b都是整数，问题就变为了有多少个a，使得K-g[x-1]*a能被g[x]整除

即：

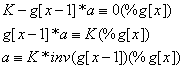
对于斐波那契数列，有一个定理，就是f[x]与f[x-1]互质（证明略复杂，在这里就不给出了），这样就保证了同余方程有解。

同时，我们还有一个限制，就是 K-g[x-1]*a > 0 (因为b>0)即 a<K/g[x-1] 的

由这两个式子，我们就可以求出对于每一个x，有多少个a，b可以使得K=a*g[x-1]+b*g[x]

酱紫，我们就可以AC这道题(≧∀≦)♪

---

Code

#include<iostream>
#include<cstdio>
using namespace std;
const int N=45;
const int n=40+2;
const int poi=1000000007;
long long f[N],K,ans;
long long exgcd(long long A,long long B,long long &x,long long &y)
{
    if(B==0)
    {
        x=1,y=0;
        return A;
    }
    long long temp=exgcd(B,A%B,x,y),tx=x;
    x=y,y=tx-(A/B)*y;
    return temp;
}
long long inv(long long A,long long POI)
{
    long long t,tt;
    exgcd(A,POI,t,tt);
    return (t%POI+POI)%POI;
}
int main()
{
    scanf("%lld",&K); 

    f[1]=f[2]=1;
    for(int i=3;i<=n;i++)
        f[i]=f[i-1]+f[i-2];
    for(int i=2;i<=n;i++)
    {
        long long a=(K*inv(f[i-1],f[i]))%f[i],to=K/f[i-1]-1;
        if(a<to)
        {
            if(a==0) ans--;
            ans=(ans+1+(to-a)/f[i])%poi;
        }
    }

    printf("%lld",ans);
    return 0;
}