【佛山市选2013】JZOJ2020年8月7日提高组T2 树环转换

【佛山市选2013】JZOJ2020年8月7日提高组T2 树环转换

题目

描述

给定一棵N个节点的树，去掉这棵树的一条边需要消耗值1，为这个图的两个点加上一条边也需要消耗值1。树的节点编号从1开始。在这个问题中，你需要使用最小的消耗值（加边和删边操作）将这棵树转化为环，不允许有重边。

环的定义如下：

• 该图有N个点，N条边。
• 每个顶点的度数为2。
• 任意两点是可达的。

树的定义如下：

• 该图有N个点，N-1条边。
• 任意两点是可达的。

数据

对于20%的数据，有1≤N≤10。

对于100%的数据，有1≤N≤1000000。

题解

题意

给出一棵树

每次删边加边的代价都为一

问最小代价将树转成环

分析

看到树呢，很容易 （个屁） 想到树形DP

但是如果直接设状态的话不好转移

思考：环是什么

不就是一条链再加上一条边吗

一条链是什么

特殊的树呀！

那么就可以设\(f[i]\)表示以\(i\)为根的子树转成链的最小代价

如果想去推方程的话，先别急

我们来看一下什么是链



一张丑陋的图

很容易发现

除了第一个和最后一个点

其他节点的度数都为2

那么是不是可以设\(f[i][0]\)表示根节点\(i\)转换成链之后是两个端点中的一个的最小代价，\(f[i][1]\)表示不管\(i\)的位置的最小代价

放方程：

告知：\(S\)表示\(\sum_\ f[son][1]\)，\(c\)表示儿子的个数，\(u,v\)是\(i\)的儿子

\(f[i][0]=min\begin{cases}S+2c\\S-(f[u][1]-f[u][0])+2*(c-1)\end{cases}\)

\(f[i][1]=min\begin{cases}f[i][0]\\S-(f[u][1]-f[u][0]+2*(c-2)\end{cases}\)

小小的优化：

对于\(u,v\)的话，既然要使更小，那么\(f[u][1]-f[u][0]\)之类的就要最大

记一下最大和次大就可以了

至于解释的话





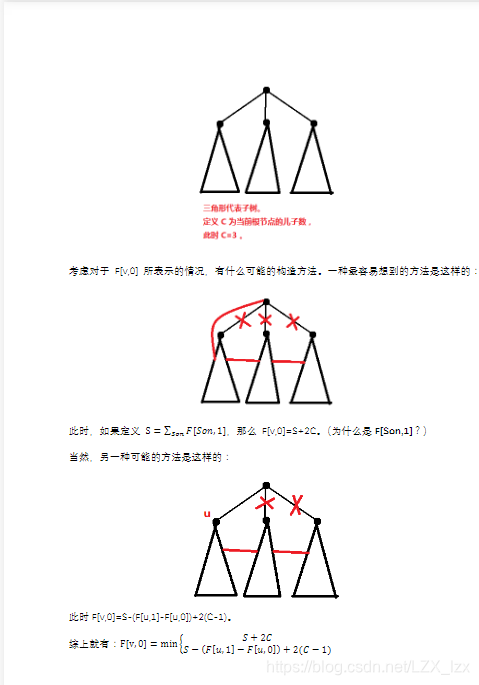
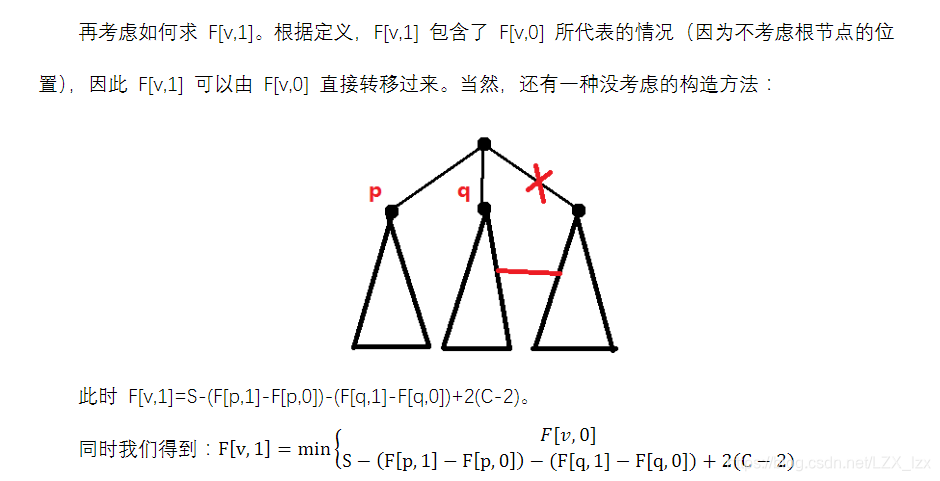
另外就是

本题卡系统栈！！！

所以你可以打\(BFS\)或者开人工栈

Code

#include<cstdio>
#include<iostream>
#define inf 99999999
using namespace std;
struct node
{
    int to,next,head;
}a[2000005];
int n,i,x,y,tot,f[1000005][3],d[1000005],father[1000005];
bool b[1000005];
void add(int x,int y)
{
    tot++;
    a[tot].to=y;
    a[tot].next=a[x].head;
    a[x].head=tot;
}
void bfs(int now)
{
    int i,j,h,t,x,mx1,mx2,s,num;
    h=0;
    t=1;
    d[1]=now;
    b[now]=true;
    while (h<t)
    {
        h++;
        for (i=a[d[h]].head;i;i=a[i].next)
        {
            x=a[i].to;
            if (b[x]==false)
            {
                t++;
                d[t]=x;
                b[x]=true;
            }
            else father[d[h]]=x;
        }
    }
    for (j=t;j;j--)
    {
        mx1=mx2=-inf;
        num=s=0;
        for (i=a[d[j]].head;i;i=a[i].next)
        {
            x=a[i].to;
            if (x!=father[d[j]])
            {
                num++;
                s+=f[x][1];
                if (f[x][1]-f[x][0]>mx1)
                {
                    mx2=mx1;
                    mx1=f[x][1]-f[x][0];
                }
                else
                {
                    if (f[x][1]-f[x][0]>mx2) mx2=f[x][1]-f[x][0];
                }
            }
        }
        f[d[j]][0]=min(s+2*num,s-mx1+2*(num-1));
        f[d[j]][1]=min(f[d[j]][0],s-mx1-mx2+2*(num-2));
    }
}
int main()
{
    freopen("T2.in","r",stdin);
    freopen("T2.out","w",stdout);
    scanf("%d",&n);
    for (i=1;i<n;i++)
    {
        scanf("%d%d",&x,&y);
        add(x,y);
        add(y,x);
    }
    bfs(1);
    printf("%d\n",min(f[1][0],f[1][1])+1);
    fclose(stdin);
    fclose(stdout);
    return 0;
}