左神算法第一节课：复杂度、排序（冒泡、选择、插入、归并）、小和问题和逆序对问题、对数器和递归（Master公式）

第一节课

• 复杂度
• 排序（冒泡、选择、插入、归并）
• 小和问题和逆序对问题
• 对数器
• 递归

1.  复杂度

认识时间复杂度常数时间的操作：一个操作如果和数据量没有关系，每次都是固定时间内完成的操作，叫做常数操作。

时间复杂度为一个算法流程中，常数操作数量的指标。常用O（读作big O）来表示。

具体来说，在常数操作数量的表达式中，只要高阶项，不要低阶项，也不要高阶项的系数，剩下的部分如果记为f(N)，那么时间复杂度为O(f(N))。

评价一个算法流程的好坏，先看时间复杂度的指标，然后再分析不同数据样本下的实际运行时间，也就是常数项时间。

举例说明：

一个有序数组A，另一个无序数组B，请打印B中的所有不在A中的数，A数组长度为N，B数组长度为M。

算法流程1：对于数组B中的每一个数，都在A中通过遍历的方式找一下；

算法流程2：对于数组B中的每一个数，都在A中通过二分的方式找一下；

算法流程3：先把数组B排序，然后用类似外排的方式打印所有在A中出现的数；

三个流程，三种时间复杂度的表达...
如何分析好坏？

算法1：O(M*N);

算法2：二分：O(M*log₂N);因为每次都砍一半，即砍了log₂N次；简写logN，默认底数为2；

算法3：双指针法，

　　1). B排序：O(M*logM);

　　2). O(N+M);描述常数操作次数的估计；

　　总：O(M*logM)+ O(N+M)

　　若M较大，N较小≈O(M*logM)

若M较小，N较大≈O(N+M)

2. 排序

1.  冒泡排序：O(N²)，额外空间复杂度为O(1);

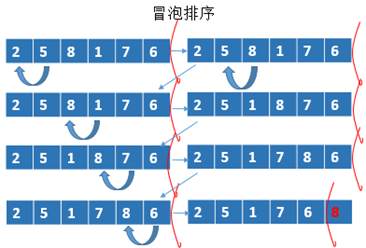
代码如下：

    public static void bubbleSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        for (int e = arr.length - 1; e > 0; e--) {
            for (int i = 0; i < e; i++) {
                if (arr[i] > arr[i + 1]) {
                    swap(arr, i, i + 1);
                }
            }
        }
    }
    public static void swap(int[] arr, int i, int j) {
        arr[i] = arr[i] ^ arr[j];
        arr[j] = arr[i] ^ arr[j];
        arr[i] = arr[i] ^ arr[j];
    }

2.  选择排序：O(N²)，额外空间复杂度为O(1);【已不用】

从剩下的的数中选择出最小/大的加入。

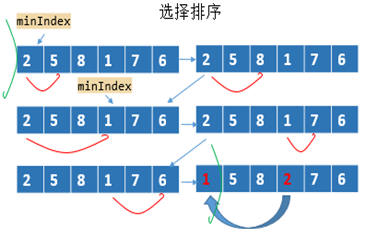
代码如下：

    public static void selectionSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        for (int i = 0; i < arr.length - 1; i++) {
            int minIndex = i;
            for (int j = i + 1; j < arr.length; j++) {
                minIndex = arr[j] < arr[minIndex] ? j : minIndex;
            }
            swap(arr, i, minIndex);
        }
    }

    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

3.  插入排序（扑克牌整牌）：O(N²)，额外空间复杂度为O(1);【经常用】

从剩下的数中选出下一个数，进行与前一位的数进行比较，然后再与前面的数比较，直到大于前一个数。

该复杂度与数据状况有关系：即实际的时间与数组的排列状况有关系，最好的情况是O(N),最差的情况是O(N²);

代码如下：

    public static void insertionSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        for (int i = 1; i < arr.length; i++) {
            for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
                swap(arr, j, j + 1);
            }
        }
    }

    public static void swap(int[] arr, int i, int j) {
        arr[i] = arr[i] ^ arr[j];
        arr[j] = arr[i] ^ arr[j];
        arr[i] = arr[i] ^ arr[j];
    }

4.   归并排序：O(N*logN)，额外空间复杂度为O(N);

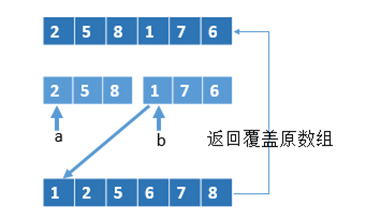
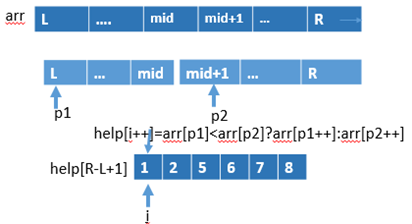
代码如下：

    public static void mergeSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        mergeSort(arr, 0, arr.length - 1);
    }

    public static void mergeSort(int[] arr, int L, int R) {
        if (L == R) {
            return;
        }
        int mid = L + ((R - L) >> 1);     //L和R中点的位置（L+R）/2
        mergeSort(arr, L, mid);           //T(n/2)
        mergeSort(arr, mid + 1, R);       //T(n/2)
        merge(arr, L, mid, R);            //O(N)
　　　　　//T(N) = 2T(N/2) + O(N)
    }

    public static void merge(int[] arr, int L, int M, int R) {
        int[] help = new int[R - L + 1];
        int i = 0;
        int p1 = L;
        int p2 = M + 1;
        while (p1 <= m && p2 <= r) {
            help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
        }
　　　　　//上述两个条件,必须有且只有一个越界，故要讨论两种情况，将剩下的跟到尾部
        while (p1 <= M) {
            help[i++] = arr[p1++];
        }
        while (p2 <= R) {
            help[i++] = arr[p2++];
        }
        for (i = 0; i < help.length; i++) {
            arr[L + i] = help[i];
        }
    }

3.  小和问题和逆序对问题：

1. 小和问题

在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。

例子：
[1,3,4,2,5]
1左边比1小的数，没有；
3左边比3小的数，1；
4左边比4小的数，1、3；
2左边比2小的数，1；
5左边比5小的数，1、3、4、2；
所以小和为1+1+3+1+1+3+4+2=16

分析：

小和问题，由当前数左侧所有比自己小的数之和相加  ==》转换为  ==》当前数右侧有多少个比自己大的，那么该数就乘以几，再相加之和；

该问题与归并排序类似：

代码如下：

    public static int smallSum(int[] arr) {
        if (arr == null || arr.length < 2) {
            return 0;
        }
        return mergeSort(arr, 0, arr.length - 1);
    }

    public static int mergeSort(int[] arr, int L, int R) {
        if (L == R) {
            return 0;
        }
        int mid = L + ((R - L) >> 1);
        return mergeSort(arr, L, mid) + mergeSort(arr, mid + 1, R) + merge(arr, L, mid, R);
    }

    public static int merge(int[] arr, int L, int M, int R) {
        int[] help = new int[r - L + 1];
        int i = 0;
        int p1 = L;
        int p2 = m + 1;
        int res = 0;//多加一个变量
        while (p1 <= M && p2 <= R) {
            res += arr[p1] < arr[p2] ? (R - p2 + 1) * arr[p1] : 0;  //多了这一句
            help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
        }
        while (p1 <= M) {
            help[i++] = arr[p1++];
        }
        while (p2 <= R) {
            help[i++] = arr[p2++];
        }
        for (i = 0; i < help.length; i++) {
            arr[L + i] = help[i];
        }
        return res;
    }

2. 逆序对问题

在一个数组中，左边的数如果比右边的数大，则这两个数构成一个逆序对，请打印所有逆序对。

4.  对数器

对数器的概念和使用

步骤：

0，有一个你想要测的方法a，

1，实现一个绝对正确但是复杂度不好的方法b，

2，实现一个随机样本产生器

3，实现比对的方法

4，把方法a和方法b比对很多次来验证方法a是否正确。

5，如果有一个样本使得比对出错，打印样本分析是哪个方法出错

6，当样本数量很多时比对测试依然正确，可以确定方法a已经正确。

5.  递归

递归就是系统栈；把当前所有变量入栈计算完后返回现场。

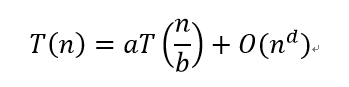
Master公式：

a是发生的次数

Over...