2016 Multi-University Training Contest 2 部分题解

　　1009，直接贪心，只要让后面的尽量小，第一位和第二位尽量大即可。

　　

　　1011，直接统计奇数的字母的个数，然后用偶数的个数平均分配到它们上面即可。代码如下：

 #include <stdio.h>
 #include <algorithm>
 #include <string.h>
 using namespace std;

 int main()
 {
     int T;
     scanf("%d",&T);
     while(T--)
     {
         int n;
         int odd = , even = ;
         scanf("%d",&n);
         for(int i=;i<=n;i++)
         {
             int t;
             scanf("%d",&t);
             if(t % )
             {
                 odd ++;
                 even += (t - ) / ;
             }
             else even += t / ;
         }
         if(odd == )
         {
             printf("%d\n",even << );
         }
         else
         {
             printf("%d\n",even / odd *  + );
         }
     }
 }

　　1001，用二次函数做即可，把阿尔法看做一个未知数。分析过程如下：

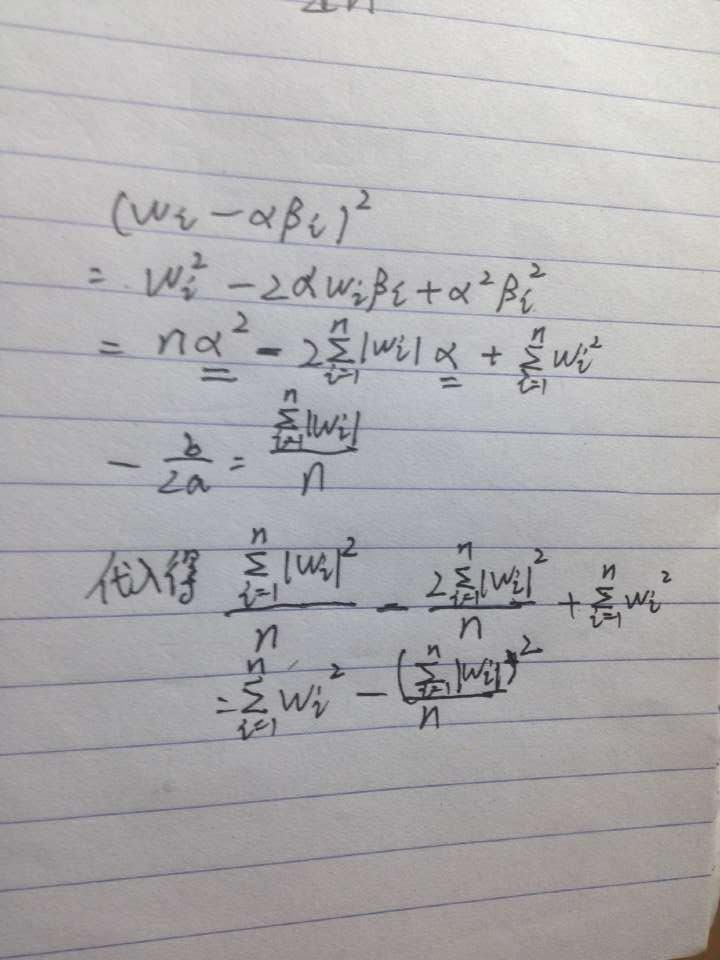
代码如下：

 #include <stdio.h>
 #include <algorithm>
 #include <string.h>
 using namespace std;
 typedef long long ll;

 int main()
 {
     int T;
     scanf("%d",&T);
     while(T--)
     {
         ll sum = , sum2 = ;
         int n;
         scanf("%d",&n);
         for(int i=;i<=n;i++)
         {
             int t;
             scanf("%d",&t);
             if(t<) t = -t; // 全部值都变正
             sum += t;
             sum2 += (ll)t*t;
         }
         sum *= sum;
         if(sum == )
         {
             printf("I64%d/%d\n",sum2,);
             continue;
         }
         ll gd = __gcd(sum,(ll)n);
         if(gd > )
         {
             sum /= gd;
             n /= gd;
         }
         sum2 *= n;
         sum2 -= sum;
         if(sum2 == )
         {
             printf("%d/%d\n",,);
             continue;
         }
         gd = __gcd(sum2,(ll)n);
         if(gd > )
         {
             sum2 /= gd;
             n /= gd;
         }
         printf("%I64d/%d\n",sum2,n);
     }
 }

　　1012，题意是匹配串和原串去匹配，原串的相应区间可以对某些位置进行操作。设位置x是可以操作的，那么x和它下一个位置进行交换；同时，两个x之间的间隔必须大于等于1。直接暴力即可，代码如下：

 #include <bits/stdc++.h>
 using namespace std;

 char s[(int)1e5+],t[+];
 char ans[(int)1e5+];
 int n,m;

 bool isok(int pos)
 {
     int j = ;
     for(int i=pos;i<=pos+m-;)
     {
         if(s[i] == t[j])
         {
             i++,j++;
         }
         else
         {

             if(i == pos+m-) return false;
             if(s[i] != t[j+] || s[i+] != t[j]) return false;
             else i += ,j += ;
         }
     }
     return true;
 }

 int main()
 {
     int T;
     scanf("%d",&T);
     while(T--)
     {
         scanf("%d%d",&n,&m);
         scanf("%s",s+);
         scanf("%s",t+);
         for(int i=;i<=n;i++) ans[i] = '';
         for(int i=;i+m-<=n;i++)
         {
             if(isok(i)) ans[i] = '';
             else ans[i] = '';
         }
         for(int i=;i<=n;i++)
         {
             printf("%c",ans[i]);
         }
         puts("");
     }
 }

　　

　　1005，找出共线的点的集合（集合内点的个数大于等于2，可以是重点）。最初的做法是，找出所有的直线方程，统计这上面的点的个数，然后这条线上的集合的个数就是C(2,m)+C(3,m)+...+C(m,m) = 2^m - m - 1。但是我们实现用了大量的map，可能是因为这一点，超时了。TLE的代码如下：

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include <map>
 #include <bits/stdc++.h>
 #define ll long long
 using namespace std;
 const int mod = (int)1e9 + ;
 //const ll p = 257;

 struct line
 {
     ll a,b,c;
     bool operator <(const line & A) const
     {
         return a==A.a?  b==A.b?c<A.c:b<A.b :a<A.a;
     }
 };
 struct point
 {
     ll x,y;
     bool operator < (const point & A) const
     {
         return x==A.x ? y<A.y :x<A.x;
     }

 }p[+];

 ll qpow(ll x,ll y)
 {
     ll ans = ;
     while(y)
     {
         if(y&) ans = ans * x % mod;
         y >>= ;
         x = (x*x) % mod;
     }
     return ans;
 }

 map<line,ll> M;
 map<point,ll> M2;
 map<line,ll> M3;
 //set<point> S;

 bool isequel(point a,point b)
 {
     if(a.x==b.x && a.y==b.y) return ;
     return ;
 }

 void get(ll &a,ll &b,ll &c,point p1,point p2)
 {
     ll x1 = p1.x,y1 = p1.y;
     ll x2 = p2.x,y2 = p2.y;
     c = x1 - x2;
     a = y1 - y2;
     b = x1*y2-y1*x2;
 }

 ll getn(ll now)
 {
     for(ll i =  ;;i++)
     {
         if(i*(i+)/ == now) return i+;
     }
 }

 void modify(ll& a , ll & b, ll &c)
 {
     if(a== && b == ) {c=;return;}
     if(b== && c == ) {a=;return;}
     if(a== && c == ) {b=;return;}
     if(a && b && c)
     {
         int gd = __gcd(a,__gcd(b,c));
         a /= gd;
         b /= gd;
         c /= gd;
     }
     else
     {
         if(a==)
         {
             int gd = __gcd(b,c);
             b /= gd;
             c /= gd;
         }
         else if(b==)
         {
             int gd = __gcd(a,c);
             a /= gd;
             c /= gd;
         }
         else if(c==)
         {
             int gd = __gcd(a,b);
             a /= gd;
             b /= gd;
         }
     }
 }

 int main()
 {
     int T;
     scanf("%d",&T);
     while(T--)
     {
         M.clear();
         M2.clear();
         M3.clear();
         //S.clear();
         int n;
         scanf("%d",&n);
         for(int i=;i<=n;i++)
         {
             ll x,y;
             scanf("%I64d%I64d",&x,&y);
             p[i] = (point){x,y};
             M2[p[i]] ++;
         }

         for(map<point,ll>::iterator it=M2.begin();it!=M2.end();it++)
         {
             map<point,ll>::iterator it2 = it;
             it2++;
             for(;it2!=M2.end();it2++)
             {
                 //if(isequel((*it).first,(*it2).first)) continue;
                 ll a,b,c;
                 get(a,b,c,(*it).first,(*it2).first);
                 modify(a,b,c);
                 M[(line){a,b,c}] += (*it).second + (*it2).second;
                 M3[(line){a,b,c}] ++;
                 //S.insert(p[i]);
                 //printf("%d %d  %d !!\n",i,j,M[(line){a,b,c}]);
             }
         }

         ll ans = ;

         for(map<line,ll>::iterator it = M.begin();it!=M.end();it++)
         {
             ll nownow = (*it).second;
             //cout << now <<"!!"<<endl;
             //ll n = now / 2;
             map<line,ll>::iterator  itt = M3.find((*it).first);
             ll now = ((*itt).second);
             //ll now = M3.second;
             ll n = getn(now);
             ll nn = nownow/(n-);
             ans += (qpow(,nn)-nn-);
             ans %= mod;
         }
         for(map<point,ll>::iterator it = M2.begin();it!=M2.end();it++)
         {
             ll now = (*it).second;
             if(now<=) continue;
             ans += (qpow(,now)-now-);
         }

         cout << ans <<endl;

     }
     return ;
 }

 /*

     5
     0 1
     0 0
     0 0
     0 1
     0 2
 */

看了标程以后觉得他的方法很好。大概是这样子的：先对所有的点按照x，y的大小排序，然后对每一个点，算出包含了这个点的的集合的个数。具体见代码和注释：

 #include <bits/stdc++.h>
 typedef long long ll;
 using namespace std;
 const int N =  + ;
 const int mod = (int)1e9 + ;

 struct point
 {
     int x, y;
     point() {}
     point(int _x, int _y): x(_x), y(_y) {}
     point operator - (const point & temp) const
     {
         return point(x - temp.x, y - temp.y);
     }
     bool operator < (const point & temp) const
     {
         return x < temp.x || (x == temp.x && y < temp.y);
     }
     bool operator == (const point & temp) const
     {
         return x == temp.x && y == temp.y;
     }
     void reduce()
     {
         int g = __gcd(abs(x), abs(y));
         if(g) {x /= g; y /= g;}
     }
 } p[N], Q[N];

 int pw[N];
 void init()
 {
     pw[] = ;
     for(int i = ; i < N; i++) pw[i] = pw[i-] *  % mod;
 }

 void update(int &x, int y)
 {
     x += y;
     if(x >= mod) x -= mod;
 }

 void run()
 {
     int n;scanf("%d", &n);
     int ans = ;
     for(int i = ; i <= n; i++) scanf("%d%d",&p[i].x, &p[i].y);
     // 先要对所有点排序，不然共线向量会有正负的区别
     sort(p + , p +  + n);
     for(int i = ; i <= n; i++)
     {
         int cnt = , tot = ;
         // cnt 是除了i这个点以外的重点的个数
         // m是 这个点位置以外的点的个数
         for(int j = i + ; j <= n; j++)
         {
             if(p[i] == p[j]) cnt++;
             else Q[++tot] = p[j] - p[i]; // Q 放的是向量
         }
         update(ans, pw[cnt] - ); // 这里是对重点们形成集合的贡献
         // 计算方式是选出i这个点，之后从剩下的cnt这么多个点中选出至少一个的种类数
         // 那么，贡献就是C(1,cnt)+C(2,cnt)+...+C(cnt,cnt) = 2^cnt - 1

         for(int j = ; j <= tot; j++) Q[j].reduce();
         sort(Q + , Q +  + tot);
         for(int x = , y; x <= tot; x = y)
         {
             for(y = x; y <= tot && Q[x] == Q[y]; y++) ;
             // y 出来的时候已经是 Q[x] != Q[y] 了，因此 y-x 正好是这一个角度上其他的点的个数
             // 这时候，对答案的贡献是，从除了i这个点以外的重点中选出任意个数的点的种类数
             // 和从这个角度上的其他点中选出至少1个点的种类数的乘积
             update(ans, 1LL * pw[cnt] * (pw[y - x] - ) % mod);
         }
     }
     printf("%d\n", ans);
 }

 int main()
 {
     init();
     int T;scanf("%d", &T);
     while(T--) run();
     return ;
 }