P3205 [HNOI2010]合唱队

题目点这里

题面：

为了在即将到来的晚会上有更好的演出效果，作为AAA合唱队负责人的小A需要将合唱队的人根据他们的身高排出一个队形。假定合唱队一共N个人，第i个人的身高为Hi米(1000<=Hi<=2000),并已知任何两个人的身高都不同。假定最终排出的队形是A 个人站成一排，为了简化问题，小A想出了如下排队的方式：他让所有的人先按任意顺序站成一个初始队形，然后从左到右按以下原则依次将每个人插入最终棑排出的队形中：

-第一个人直接插入空的当前队形中。

-对从第二个人开始的每个人，如果他比前面那个人高(H较大)，那么将他插入当前队形的最右边。如果他比前面那个人矮(H较小)，那么将他插入当前队形的最左边。

当N个人全部插入当前队形后便获得最终排出的队形。

例如，有6个人站成一个初始队形，身高依次为1850、1900、1700、1650、1800和1750,

那么小A会按以下步骤获得最终排出的队形：

1850

• 1850 , 1900 因为 1900 > 1850

• 1700, 1850, 1900 因为 1700 < 1900

• 1650 . 1700, 1850, 1900 因为 1650 < 1700

• 1650 , 1700, 1850, 1900, 1800 因为 1800 > 1650

• 1750， 1650, 1700，1850, 1900, 1800 因为 1750 < 1800

因此，最终排出的队形是 1750，1650，1700，1850, 1900，1800

小A心中有一个理想队形，他想知道多少种初始队形可以获得理想的队形

大概思路：从最后的结果来看，队尾或队头一定是最后入队的，所以每次都分离队头和队尾，分别讨论他们的状态求解。（动规）

这个思路有点抽象。。举个例子解释一下 （以输入 1 2 3 5 4 作为例子）

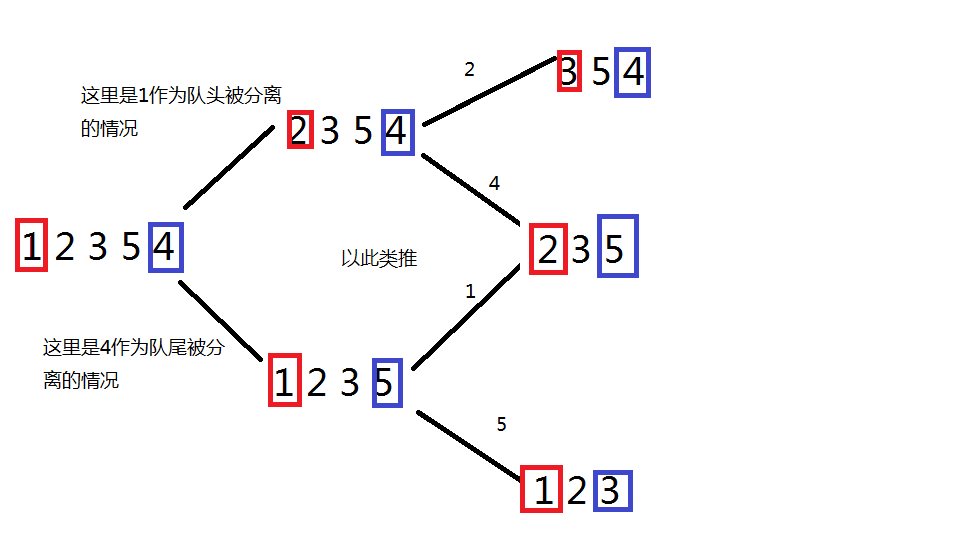
真的就是这么简单的分下去吗？

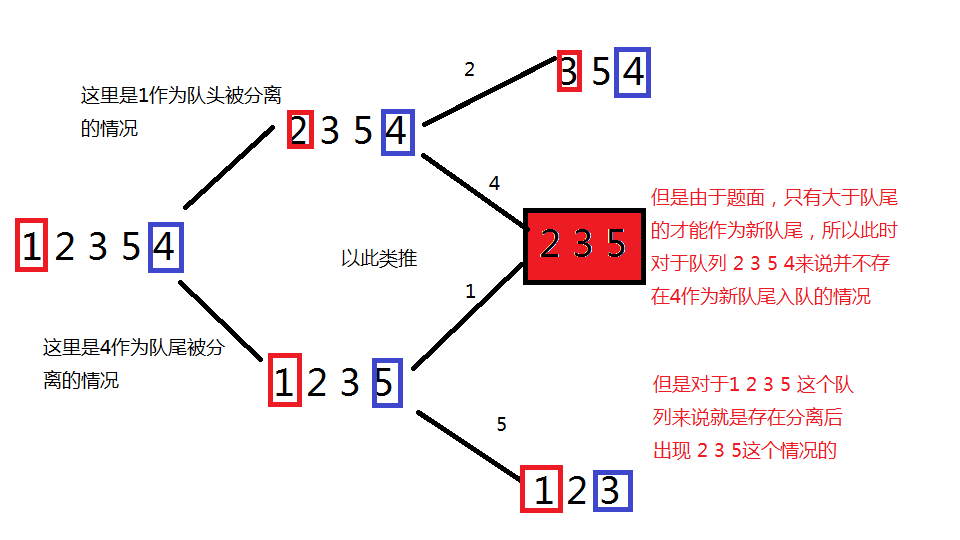
这个问题怎么解决呢？

这时，我们假设当前要讨论的数为x，删去x的队列队头值为L,队尾值为R。就能发现

x作为新队尾时也是同理（这里就不写了）

所以可以根据上图推出动态转移方程式

我们设队列为q[],方案数存储在dp[][][]中。

for(int len=n-;len>=;len--)
    {
        for(int l=,r=len;r<=n;l++,r++)
        {
            dp[l][r][]=((q[l]<q[r+])*dp[l][r+][]+(q[l-]<q[l])*dp[l-][r][])%Mod;
            dp[l][r][]=((q[r]>q[l-])*dp[l-][r][]+(q[r]<q[r+])*dp[l][r+][])%Mod;
        }
    }

这里的0代表作为队头入队，1代表作为队尾入队。

最重要的部分到这里就结束啦！

下面是代码

#include<iostream>
#include<cstdio>
using namespace std;
int dp[][][];
int q[];
int Mod=;
int n;
int main()
{
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        scanf("%d",&q[i]);
    }
    q[]=Mod;
    q[n+]=-Mod;
    dp[][n][]=dp[][n][]=;
    for(int len=n-;len>=;len--)
    {
        for(int l=,r=len;r<=n;l++,r++)
        {
            dp[l][r][]=((q[l]<q[r+])*dp[l][r+][]+(q[l-]<q[l])*dp[l-][r][])%Mod;
            dp[l][r][]=((q[r]>q[l-])*dp[l-][r][]+(q[r]<q[r+])*dp[l][r+][])%Mod;
        }
    }
    int ans=;
    for(int i=;i<=n;i++)
    {
        ans=(ans+dp[i][i][])%Mod;//这里直接输出dp[1][n][0]+dp[1][n][1]也行
    }
    printf("%d",ans);
    return ;
 } 

蒟蒻的第一篇博客！（放个礼花吧先）