Apriori 算法python实现

1. Apriori算法简介

Apriori算法是挖掘布尔关联规则频繁项集的算法。Apriori算法利用频繁项集性质的先验知识，通过逐层搜索的迭代方法，即将K-项集用于探察(k+1)项集，来穷尽数据集中的所有频繁项集。先找到频繁项集1-项集集合L1， 然后用L1找到频繁2-项集集合L2，接着用L2找L3，知道找不到频繁K-项集，找到每个L_k需要一次数据库扫描。注意：频繁项集的所有非空子集也必须是频繁的。Apriori性质通过减少搜索空间，来提高频繁项集逐层产生的效率。Apriori算法由连接和剪枝两个步骤组成。

2. Apriori算法步骤

根据一个实例来解释：下图是一个交易单，I1至I5可看作5种商品。下面通过频繁项集合来找出关联规则。

假设我们的最小支持度阈值为2，即支持度计数小于2的都要删除。

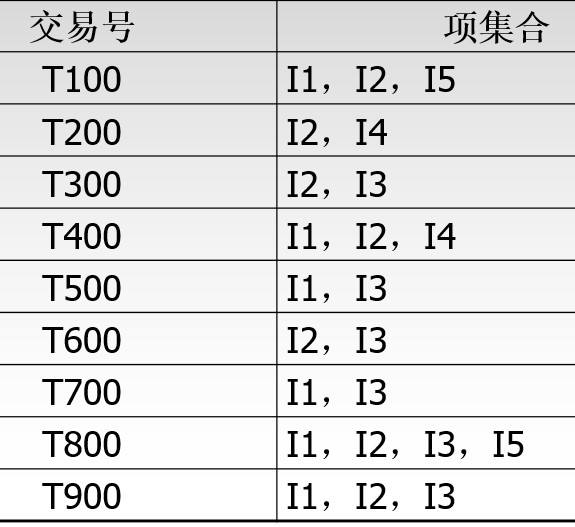
上表第一行（第一项交易）表示：I1和I2和I5一起被购买。

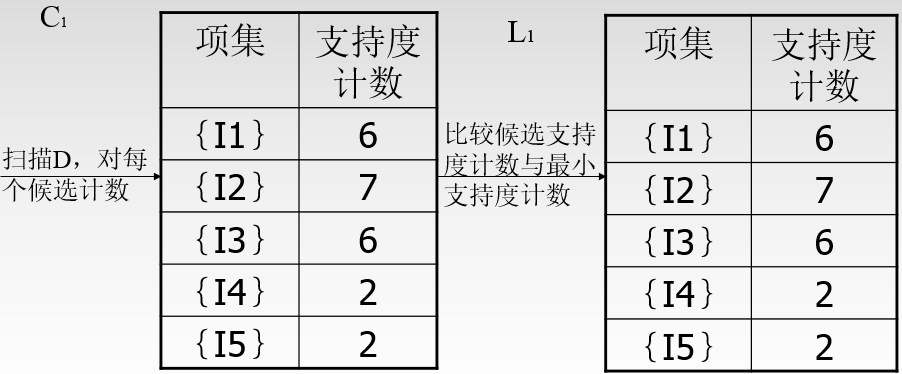
C1至L1的过程： 只需查看支持度是否高于阈值，然后取舍。上图C1中所有阈值都大于2，故L1中都保留。

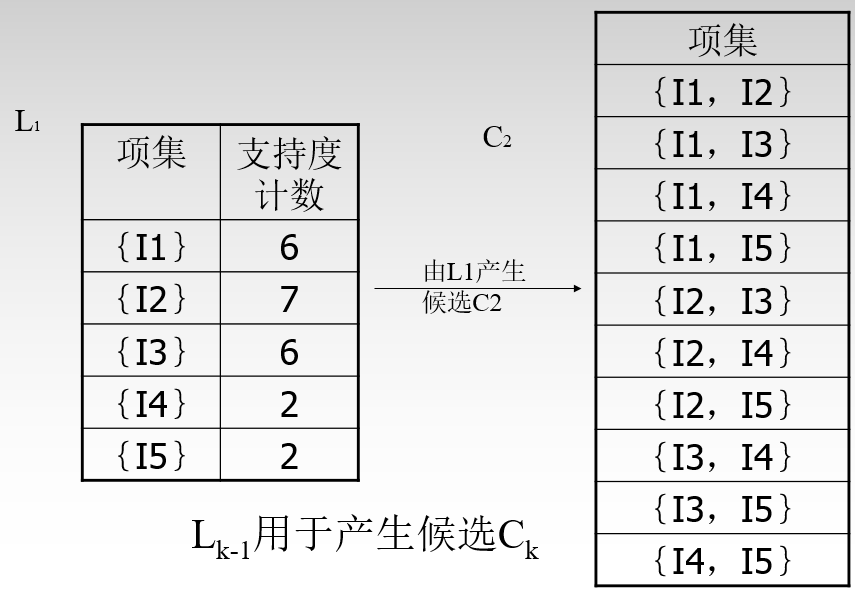
L1至C2的过程分三步：

• 遍历产生L1中所有可能性组合，即（I1,I2）...（I4,I5 )
• 对便利产生的每个组合进行拆分，以保证频繁项集的所有非空子集也必须是频繁的。即对于（I1，I2）来说进行拆分为I1，I2.由于I1和I2在L1中都为频繁项，所以这一组合保留。
• 对于剩下的C2根据原数据集中进行支持度计数

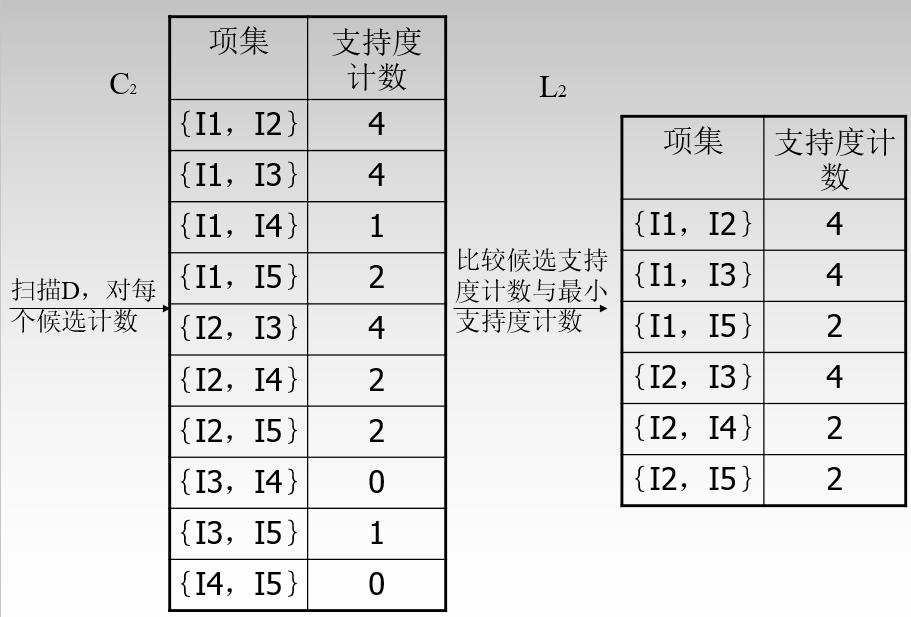
C2至L2的过程： 只需查看支持度是否高于阈值，然后取舍。

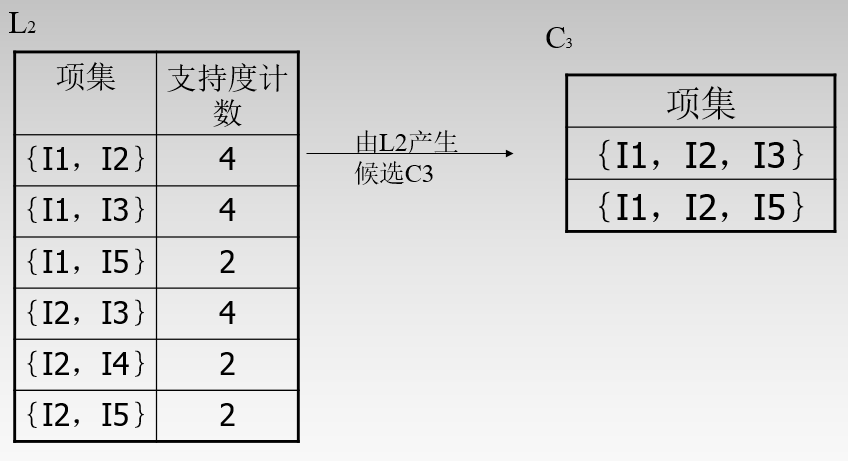
L2至C3的过程：

还是上面的步骤。首先生成（1，2，3）、（1，2，4）、（1，2，5）....为什么最后只剩（1，2，3）和（1，2，5）呢？因为剪枝过程：（1，2，4）拆分为（1，2）和（1，4）和（2，4）.然而（1，4）在L2中不存在，即非频繁项。所有剪枝删除。然后对C3中剩下的组合进行计数。发现（1，2，3）和（1，2，5）的支持度2。迭代结束。

所以算法过程就是 C_k - L_k - C_k+1 的过程：

3.Apriori算法实现

# -*- coding: utf-8 -*-
"""
Created on Sat Dec  9 15:33:45 2017

@author: LPS
"""

import numpy as np
from itertools import combinations  # 迭代工具

data = [[1,2,5], [2,4], [2,3], [1,2,4], [1,3], [2,3], [1,3], [1,2,3,5], [1,2,3]]
minsp = 2

d = []
for i in range(len(data)):
    d.extend(data[i])
new_d = list(set(d))

def satisfy(s, s_new, k):  # 更新确实存在的L

    e =[]
    ss_new =[]
    for i in range(len(s_new)):
        for j in combinations(s_new[i], k):  # 迭代产生所有元素可能性组合
            e.append(list(j))
        if ([l for l in e if l not in s]) ==[] :
            ss_new.append(s_new[i])
        e = []

    return ss_new  # 筛选满足条件的结果

def count(s_new):  # 返回narray格式的C
    num = 0
    C = np.copy(s_new)
    C = np.column_stack((C, np.zeros(C.shape[0])))

    for i in range(len(s_new)):
        for j in range(len(data)):
            if ([l for l in s_new[i] if l not in data[j]]) ==[] :
                num = num+1
        C[i,-1] = num
        num = 0          

    return C

def limit(L):  # 删掉不满足阈值的C
    row = []
    for i in range(L.shape[0]):
        if L[i,-1] < minsp :
            row.append(i)
    L = np.delete(L, row, 0) 

    return L

def generate(L, k):  # 实现由L至C的转换
    s = []
    for i in range(L.shape[0]):
        s.append(list(L[i,:-1]))
    s_new = []
#    L = L.delete(L, -1, 1)
#    l = L.shape[1]
    for i in range(L.shape[0]-1):
        for j in range(i+1, L.shape[0]):
            if (L[j,-2]>L[i,-2]):
                t = list(np.copy(s[i]))
                t.append(L[j,-2])
                s_new.append(t)  # s_new为列表

    s_new = satisfy(s, s_new, k) 

    C = count(s_new)

    return C

# 初始的C与L
C = np.zeros([len(new_d), 2])
for i in range(len(new_d)):
    C[i:] = np.array([new_d[i], d.count(new_d[i])])

L = np.copy(C)
L = limit(L)

# 开始迭代
k = 1
while (np.max(L[:,-1]) > minsp):
    C = generate(L, k)  # 由L产生C
    L = limit(C)        # 由C产生L
    k = k+1

# 对最终结果去重复

print((list(set([tuple(t) for t in L])))
# 结果为   [(1.0, 2.0, 3.0, 2.0), (1.0, 2.0, 5.0, 2.0)]