[Jobdu] 题目1385：重建二叉树

根据一棵二叉树的先序遍历和后序遍历，重建二叉树

例子：

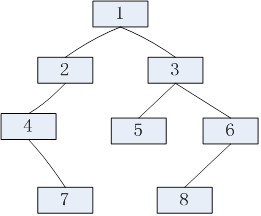
我们先来看一个例子，二叉树如上图，则先序遍历为：1 2 4 7 3 5 6 8，中序遍历为：4 7 2 1 5 3 8 6

思路：

先序遍历中的第一个元素为根节点，这个元素将中序遍历划分为左右两个部分，左边的为左子树的中序遍历，右边的为右子树的中序遍历，同样也可以将先序遍历除了第一个元素以外的划分为两个部分，第一个部分是左子树的先序遍历，第二部分是右子树的先序遍历。

由此可知，这是一个递归过程，可以利用递归函数来构建二叉树。对于二叉树的这种常见操作要熟悉，实现的代码要会写。

代码：

 #include <stdio.h>
 #include <stdlib.h>
 
 // the binary tree node
 typedef struct BTNode{
     int key;
     struct BTNode *lchild;
     struct BTNode *rchild;
 }BTNode;
 
 // find the key in the InOrder array, if not finded then return -1
 int findKey(int arr[], int start, int end, int key) {
     int i;
     for (i = start; i <= end; i++)
         if (arr[i] == key)
             return i;
     return -;
 }
 
 // create the binary tree by PreOrder and InOrder
 BTNode *rebuildTree(int pre[], int startPre, int endPre, int in[], int startIn, int endIn) {
     // both order have the same size
     if (endPre - startPre != endIn - startIn)
         return NULL;
     // the root is the first node of PreOrder
     BTNode *root = (BTNode *) malloc(sizeof(BTNode));
     root->key = pre[startPre];
     root->lchild = NULL;
     root->rchild = NULL;
 
     // find the index of root node in the InOrder
     int mid = findKey(in, startIn, endIn, pre[startPre]);
     if (mid == -)
         return NULL;
 
     // if the left-subtree exists, create left-subtree
     int length;
     if (mid > startIn) {
         length = mid - startIn;
         root->lchild = rebuildTree(pre, startPre + , startPre +  + length - , in, startIn, startIn + length - );
     }
 
     // if the right-subtree exists, create right-subtree
     if (mid < endIn) {
         length = endIn - mid;
         root->rchild = rebuildTree(pre, endPre - length + , endPre, in, endIn - length + , endIn);
     }
 
     return root;
 }
 
 void postTraverse(BTNode *tree) {
     if (tree) {
         postOrder(tree->lchild);
         postOrder(tree->rchild);
         printf("%d ", tree->key);
     }
 }
 
 int main() {
     int preOrder[] = {, , , , , , , };
     int inOrder[] = {, , , , , , , };
     BTNode *root = rebuildTree(preOrder, , , inOrder, , );
     postTraverse(root);
     printf("\n");
 
     return ;
 }