《A First Course in Probability》-chaper5-连续型随机变量-基本概念

在利用基本的概率论模型解决实际问题的时候，我们很容易发现一些随机变量的连续分布的，例如火车进站的时间、台灯的寿命等一些和时间相关的随机变量，此时我们发现我们难以求出某个点的概率了，因为随机变量是连续的，基本事件空间是一个无穷的空间，而与无限、连续这些字眼相关，很自然的想到，这里我们要借助积分的工具。

现在我们面临的问题是，如何用上积分这个工具呢？我们假想一条曲线f(x)和连续随机变量的取值区间[a,b]围成了一个面积为1的曲边梯形，（之所以控制面积为1，是为了满足分布列的基本性质），那么对于P(c≤X≤d)，就等于f(x)在[c,d]的定积分。

容易看到对于不同问题的分布列，这样一个曲边梯形中的f(x)和分布列自身是构成一一映射的，我们称f(x)是连续随机变量X的概率密度曲线。

基于这些东西，我们可以很好地给连续随机变量下一个定义了：

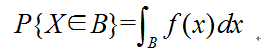
满足这样的概率分布的分布列的随机变量X成为连续性随机变量(其中B是表示取值范围的集合)。

Ex1 (uva 11346)：

给出一个区域[-a,b] , [-b,b]，给出面积S，问在该区域内任选一点P，使得P和坐标原点为对角线的矩形的面积大于S的概率是多少。

分析：

很典型的几何概型问题或者说连续型随机变量，这里需要注意的是，定积分求解出一个结果会出现ln，要保证ln在程序中运算有意义，所以它的真数要大于0.