Spring 01 概述

简介

Spring 是开源的轻量级 J2EE 框架

我们常说的 Spring 实际上是指 Spring Framework，它是 Spring 家族中的一个重要分支。

官方文档

https://docs.spring.io/spring-framework/docs/current/reference/html/core.html

两大核心：IOC 和 AOP

IOC

Inversion of Control，即控制反转，把创建对象的过程交给 Spring 进行管理。

实现方式

DI（Dependency Injection），即依赖注入。

底层实现

工厂模式 + XML 解析 + 反射

AOP

Aspect Oriented Programming，即面向切面编程，不修改源代码进行功能增强。

底层实现

动态代理 => 代理模式 => 反射

结构

组件

Spring 中的组件分别提供一块特定的功能。

core

spring-core

核心组件，依赖注入的最基本实现。

spring-beans

Bean 工厂与 Bean 的装配，提供控制反转的基础实现。

spring-context

上下文即 IOC 容器，在 IOC 基础上继续扩展服务。

spring-expression

对表达式语言的支持。

commons-logging

因为 spring-core 依赖了 commons-logging，而其他模块都依赖了 spring-core。

所以整个 Spring 框架都依赖了 commons-logging。

如果有自己的日志实现如 log4j，可以排除对 commons-logging 的依赖，没有日志实现而排除了 commons-logging 依赖，会编译报错。

<dependency>
    <groupId>org.springframework</groupId>
    <artifactId>spring-context</artifactId>
    <version>3.2.17.RELEASE</version>
    <exclusions>
        <exclusion>
            <groupId>commons-logging</groupId>
            <artifactId>commons-logging</artifactId>
        </exclusion>
    </exclusions>
</dependency>

aop

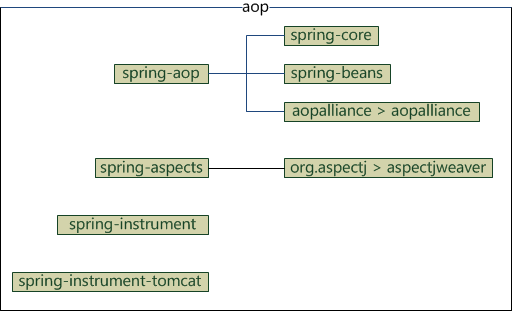
spring-aop

提供面向切面编程的实现。

spring-aspects

提供对 AspectJ 框架的整合。

spring-instrument

提供一些类级的工具支持和 ClassLoader 级的实现，用于服务器。

spring-instrument-tomcat

针对 Tomcat 的 instrument 实现。

data access

spring-jdbc

JDBC 的支持。

spring-tx

事务控制。

spring-orm

对象关系映射，集成 ORM 框架。

spring-oxm

对象 XML 映射。

spring-jms

Java 消息服务。

web

spring-web

基础 web 功能，如文件上传。

spring-webmvc

MVC 实现。

spring-webmvc-portlet

基于 portlet 的 MVC 实现。

spring-websocket

对 WebSocket 的支持，为 WEB 应用提供的高效通信工具。

test

spring-test

测试，提供 jUnit 与 mock 测试功能。

spring-context-support

对 spring-context 的扩展。

Spring 额外支持包，比如邮件服务、视图解析等。

其他

spring-messaging

对消息服务的支持，例如搭配 JMS、搭配 AMQP、搭配 WebSocket 等，用于构建基于消息的应用程序。