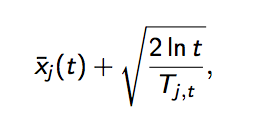通俗bandit算法

[原文链接]

选择是一个技术活

著名鸡汤学家沃.滋基硕德曾说过：选择比努力重要。

我们会遇到很多选择的场景。上哪个大学，学什么专业，去哪家公司，中午吃什么，等等。这些事情，都让选择困难症的我们头很大。那么，有办法能够应对这些问题吗？

答案是：有！而且是科学的办法，而不是“走近科学”的办法。那就是bandit算法！

bandit算法来源于人民群众喜闻乐见的赌博学，它要解决的问题是这样的[1]：

一个赌徒，要去摇laohu机，走进赌场一看，一排laohu机，外表一模一样，但是每个laohu机吐钱的概率可不一样，他不知道每个laohu机吐钱的概率分布是什么，那么想最大化收益该怎么整？这就是多臂赌博机问题(Multi-armed bandit problem, K-armed bandit problem, MAB)。

怎么解决这个问题呢？求菩萨？拜赌神？都不好使，最好的办法是去试一试，而这个试一试也不是盲目地试，而是有策略地试，越快越好，这些策略就是bandit算法。

这个多臂问题，它是一个可以装下很多问题的万能框：

1. 假设一个用户对不同类别的内容感兴趣程度不同，那么我们的推荐系统初次见到这个用户时，怎么快速地知道他对每类内容的感兴趣程度？这就是推荐系统的冷启动。

2. 假设我们有若干广告库存，怎么知道该给每个用户展示哪个广告，从而获得最大的点击收益？是每次都挑效果最好那个么？那么新广告如何才有出头之日？

3. 我们的算法工程师又想出了新的模型，有没有比A/B test更快的方法知道它和旧模型相比谁更靠谱？

4. ...

全都是关于选择的问题。只要是关于选择的问题，都可以简化成一个多臂赌博机问题，毕竟小赌怡情嘛，人生何处不赌博。

特别提出，在计算广告和推荐系统领域，针对这个问题，还有个说法叫做EE问题：exploit－explore问题。

exploit意思就是：比较确定的兴趣，当然要用啊。好比说我们已经挣到的钱，当然要花啊；

explore意思就是：不断探索用户新的兴趣才行，不然很快就会出现一模一样的反复推荐。就好比我们虽然有一点钱可以花了，但是还得继续搬砖挣钱啊，不然花完了喝西北风啊。

bandit算法哪家强

现在来一本正经地介绍一下bandit算法怎么解决这类问题的。

我们的选择到底有多遗憾？

王家卫在《一代宗师》里寄出一句台词：

人生要是无憾，那多无趣

本文作者说：

算法要是无憾，那应该是过拟合了。

其实我想引出的是：怎么衡量不同bandit算法解决多臂问题的好坏？多臂问题里有一个概念叫做累计遗憾(regret)[2]

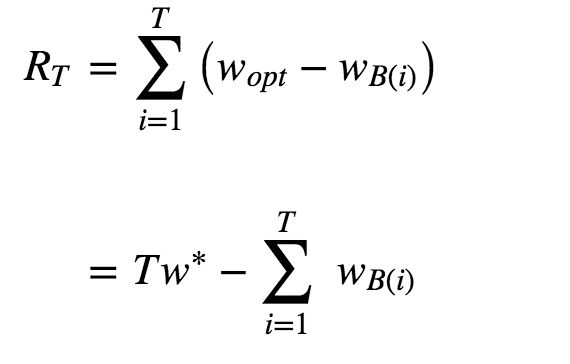
解释一下这个公式：

首先，这里我们讨论的每个臂的收益非0即1，也就是伯努利收益。

公式1最直接：每次选择后，上帝都告诉你，和本该最佳的选择差了多少，然后把每次差距累加起来就是总的遗憾。

wB(i)是第i次试验时被选中臂的期望收益， w\*是所有臂中的最佳那个，如果上帝提前告诉你，我们当然每次试验都选它，问题是上帝不告诉你，所以我们就有了这篇文章。

这个公式可以用来对比不同bandit算法的效果：对同样的多臂问题，用不同的bandit算法试验相同次数，看看谁的regret增长得慢。

本着大家可以直接堆代码的原则，所以本文跳过一切数学上的分析，赤裸裸地陈列出最常用的几个bandit算法。

几个bandit算法

第一个，Thompson sampling算法。这个算法我喜欢它，因为它只有一行代码就可以实现。

简单介绍一下它的原理：

假设每个臂是否产生收益，其背后有一个概率分布，产生收益的概率为p

我们不断地试验，去估计出一个置信度较高的*概率p的概率分布*就能近似解决这个问题了。

怎么能估计概率p的概率分布呢？ 答案是假设概率p的概率分布符合beta(wins, lose)分布，它有两个参数: wins, lose。

每个臂都维护一个beta分布的参数。每次试验后，选中一个臂，摇一下，有收益则该臂的wins增加1，否则该臂的lose增加1。

每次选择臂的方式是：用每个臂现有的beta分布产生一个随机数b，选择所有臂产生的随机数中最大的那个臂去摇。

以上就是Thompson采样，用python实现就一行：

choice = numpy.argmax(pymc.rbeta(1 + self.wins, 1 + self.trials - self.wins))

第二个是UCB算法，UCB算法全称是Upper Confidence Bound(置信区间上界)，不多说了，它的算法步骤如下[4]：

先对每一个臂都试一遍

之后，每次选择以下值最大的那个臂

其中加号前面是这个臂到目前的收益均值，后面的叫做bonus，本质上是均值的标准差，t是目前的试验次数，Tjt是这个臂被试次数。

这个公式反映：均值越大，标准差越小，被选中的概率会越来越大，起到了exploit的作用；同时哪些被选次数较少的臂也会得到试验机会，起到了explore的作用。

第三个是Epsilon-Greedy算法。这是一个朴素的算法，也很简单有效，有点类似模拟退火：

选一个(0,1)之间较小的数epsilon

每次以概率epsilon（产生一个[0,1]之间的随机数，比epsilon小）做一件事：所有臂中随机选一个。否则，选择截止当前，平均收益最大的那个臂。

是不是简单粗暴？epsilon的值可以控制对Exploit和Explore的偏好程度。越接近0，越保守，只想花钱不想挣钱。

最后还有一个完全是朴素的：

先试几次，每个臂都有了均值之后，一直选均值最大那个臂。这个算法是我们人类在实际中最常采用的，不可否认，它还是比随机乱猜要好。

以上五个算法，我们用10000次模拟试验的方式对比了其效果如图，原始代码来源[5]：

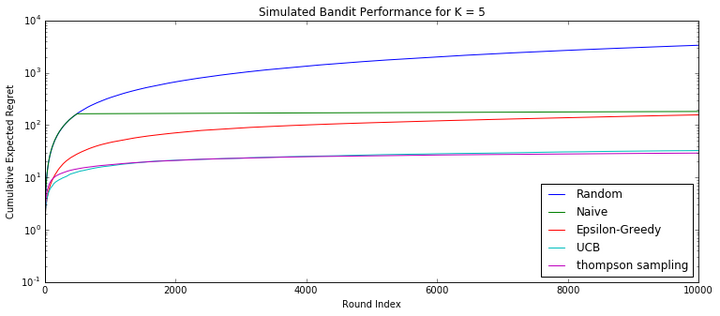
算法效果对比一目了然：UCB算法和Thompson采样算法显著优秀一些。

至于你实际上要选哪一种bandit算法，你可以选一种bandit算法来选bandit算法。。。

用bandit算法解决推荐系统冷启动的简单思路

我想，屏幕前的你已经想到了，推荐系统冷启动可以用bandit算法来解决一部分。

大致思路如下：

用分类或者Topic来表示每个用户兴趣，我们可以通过几次试验，来刻画出新用户心目中对每个topic的感兴趣概率。

这里，如果用户对某个topic感兴趣，就表示我们得到了收益，如果推给了它不感兴趣的topic，推荐系统就表示很遗憾(regret)了。

当一个用户来了，针对这个用户，我们用Thompson算法为每一个topic采样一个随机数，排序后，输出采样值top N 的推荐item。注意，这里略有改动，原始多臂问题每次只摇一个臂，我们这里一次摇N个臂。

获取用户的反馈，比如点击。没有反馈则更新对应topic的lose值，点击了则更新对应topic的wins值。