洛谷 P 3371 单元最短路

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式：

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例

输入样例#1：

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出样例#1：

0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15

对于40%的数据：N<=100，M<=10000

对于70%的数据：N<=1000，M<=100000

对于100%的数据：N<=10000，M<=500000

样例说明：

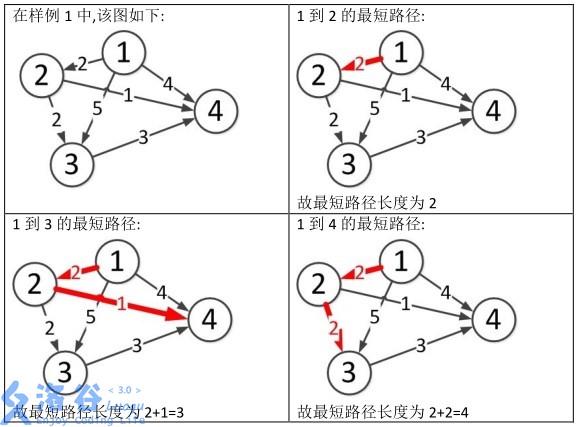
60分SPFA代码存档：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<queue>
 #define MAXN 2147483647
 #define N 10010
 using namespace std;
 struct node{
     int u,v,w;
     int next;
 }e[];
 int n,m,s,head[N],dis[N],ei;
 bool exist[N];
 void add(int u,int v,int w){
     e[++ei].u=u;e[ei].v=v;e[ei].w=w;
     e[ei].next=head[u];head[u]=ei;
 }
 queue<int> q;
 int main()
 {
     scanf("%d%d%d",&n,&m,&s);
     memset(dis,0x3f3f3f3f,sizeof(dis));
     memset(exist,false,sizeof(exist));
     for(int i=,x,y,z;i<=m;i++){
         scanf("%d%d%d",&x,&y,&z);
         add(x,y,z);
     }
     exist[s]=true;dis[s]=;q.push(s);
     while(!q.empty()){
         int p=q.front();q.pop();exist[p]=false;
         for(int i=head[p];i;i=e[i].next){
             int v=e[i].v;
             if(dis[v]>dis[p]+e[i].w){
                 dis[v]=dis[p]+e[i].w;
                 if(!exist[v]){
                     q.push(v);
                     exist[v]=true;
                 }
             }
         }
     }
     for(int i=;i<=n;i++){
         if(dis[i]==0x3f) printf("%d ",MAXN);
         else printf("%d ",dis[i]);
     }
     return ;
 }

head数组开大一点，就成90了

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<queue>
 #define MAXN 2147483647
 #define N 10010
 using namespace std;
 struct node{
     int u,v,w;
     int next;
 }e[];
 int n,m,s,head[],ei;
 long long dis[N];
 bool exist[N];
 void add(int u,int v,int w){
     e[++ei].u=u;e[ei].v=v;e[ei].w=w;
     e[ei].next=head[u];head[u]=ei;
 }
 queue<int> q;
 int main()
 {
     scanf("%d%d%d",&n,&m,&s);
     memset(dis,0x3f3f3f3f,sizeof(dis));
     memset(exist,false,sizeof(exist));
     for(int i=,x,y,z;i<=m;i++){
         scanf("%d%d%d",&x,&y,&z);
         add(x,y,z);
     }
     exist[s]=true;dis[s]=;q.push(s);
     while(!q.empty()){
         int p=q.front();q.pop();exist[p]=false;
         for(int i=head[p];i;i=e[i].next){
             int v=e[i].v;
             if(dis[v]>dis[p]+e[i].w){
                 dis[v]=dis[p]+e[i].w;
                 if(!exist[v]){
                     q.push(v);
                     exist[v]=true;
                 }
             }
         }
     }
     for(int i=;i<=n;i++){
         if(dis[i]==0x3f3f3f3f) printf("%lld ",MAXN);
         else printf("%lld ",dis[i]);
     }
     return ;
 }