AC日记——联合权值洛谷 P1351

题目描述

无向连通图G 有n 个点，n - 1 条边。点从1 到n 依次编号，编号为 i 的点的权值为W i ，每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ，若它们的距离为2 ，则它们之间会产生Wu

×Wv 的联合权值。

请问图G 上所有可产生联合权值的有序点对中，联合权值最大的是多少？所有联合权值之和是多少？

输入输出格式

输入格式：

输入文件名为link .in。

第一行包含1 个整数n 。

接下来n - 1 行，每行包含 2 个用空格隔开的正整数u 、v ，表示编号为 u 和编号为v 的点之间有边相连。

最后1 行，包含 n 个正整数，每两个正整数之间用一个空格隔开，其中第 i 个整数表示图G 上编号为i 的点的权值为W i 。

输出格式：

输出文件名为link .out 。

输出共1 行，包含2 个整数，之间用一个空格隔开，依次为图G 上联合权值的最大值

和所有联合权值之和。由于所有联合权值之和可能很大，[b]输出它时要对10007 取余。 [/b]

输入输出样例

输入样例#1：

输出样例#1：

20 74

说明

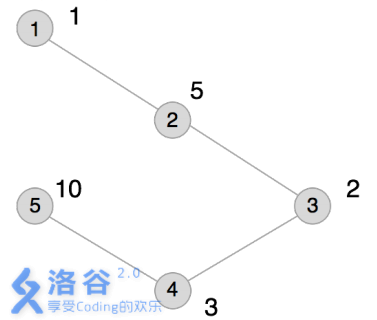
本例输入的图如上所示，距离为2 的有序点对有( 1,3) 、( 2,4) 、( 3,1) 、( 3,5) 、( 4,2) 、( 5,3) 。

其联合权值分别为2 、15、2 、20、15、20。其中最大的是20，总和为74。

【数据说明】

对于30% 的数据，1 < n≤ 100 ；

对于60% 的数据，1 < n≤ 2000；

对于100%的数据，1 < n≤ 200 , 000 ，0 < wi≤ 10, 000 。

思路：

　　对于每个点处理父亲节点和子节点

　　即把他们的dis求和作为这个点的sum

　　还用他们的max和max_

　　用一次dfs处理

　　然后第二次dfs

　　求ans_sum和ans_max；

　　轻松ac

来，上代码：

#include <cstdio>

#include <iostream>

#include <algorithm>

#define mod 10007

#define maxn 200001

using namespace std;

struct TreeNodeType {

    int f,dis,max_,flag,max__;

    long long int sum;

};

struct TreeNodeType tree[maxn];

struct EdgeType {

    int to,next;

};

struct EdgeType edge[maxn<<];

int if_z,n,head[maxn],num,ans_s,ans_m;

char Cget;

inline void read_int(int &now)

{

    now=,if_z=,Cget=getchar();

    while(Cget>''||Cget<'')

    {

        if(Cget=='-') if_z=-;

        Cget=getchar();

    }

    while(Cget>=''&&Cget<='')

    {

        now=now*+Cget-'';

        Cget=getchar();

    }

    now*=if_z;

}

inline void edge_add(int from,int to)

{

    edge[++num].to=from,edge[num].next=head[to],head[to]=num;

    edge[++num].to=to,edge[num].next=head[from],head[from]=num;

}

void search(int now,int fa)

{

    tree[now].f=fa,tree[now].max_=tree[fa].dis;

    tree[now].flag=fa,tree[now].sum+=tree[fa].dis;

    for(int i=head[now];i;i=edge[i].next)

    {

        if(edge[i].to==fa) continue;

        tree[now].sum+=tree[edge[i].to].dis;

        if(tree[edge[i].to].dis>tree[now].max_)

        {

            tree[now].flag=edge[i].to;

            tree[now].max_=tree[edge[i].to].dis;

        }

        search(edge[i].to,now);

    }

    for(int i=head[now];i;i=edge[i].next)

    {

        if(edge[i].to==tree[now].flag) continue;

        tree[now].max__=max(tree[now].max__,tree[edge[i].to].dis);

    }

}

void search_(int now)

{

    if(tree[now].f!=)

    {

        tree[tree[now].f].sum-=tree[now].dis;

        ans_s=(ans_s+(tree[now].dis)*tree[tree[now].f].sum)%mod;

        if(tree[tree[now].f].flag!=now) ans_m=max(ans_m,tree[now].dis*tree[tree[now].f].max_);

        else ans_m=max(ans_m,tree[now].dis*tree[tree[now].f].max__);

    }

    for(int i=head[now];i;i=edge[i].next)

    {

        if(edge[i].to==tree[now].f) continue;

        search_(edge[i].to);

    }

}

int main()

{

    read_int(n);

    int from,to;

    for(int i=;i<n;i++)

    {

        read_int(from),read_int(to);

        edge_add(from,to);

    }

    for(int i=;i<=n;i++) read_int(tree[i].dis);

    search(,),search_();

    cout<<ans_m<<' '<<(ans_s<<)%mod<<endl;

    return ;

}