Matlab 霍夫变换 ( Hough Transform） 直线检测

PS：好久没更新，因为期末到了，拼命复习中。复习久了觉得枯燥，玩玩儿霍夫变换直线检测

霍夫变换的基本原理不难，即便是初中生也很容易理解（至少在直线检测上是这样子的）。

霍夫变换直线检测的基本原理：（不配图了，自己在白纸上画画，理解更深刻）

一步一步来：

1、在白纸上画出一个直角坐标系，任意给出一个点；

2、那么，对于点（x0,y0）,经过这个点的直线必定满足y0=k*x0+b, 其中k是直线的斜率，b是直线的截距；

3、上式可以化成b=y0-k*x0,  可以看作是以-x0为斜率，以y0为截距，在k-b空间上的一个直线方程（k，b为变量）；

4、可见，k-b空间上的一条直线， 代表了x-y空间经过特定点的所有直线，而x-y上的特定直线责备k-b空间上的特定点表示；

利用这个原理，我们可以通过一下方法检测可能出线的直线：

1、得到一副边缘图像；

2、对图像中的每一个边缘点，在k-b空间中画出一条直线；

3、在各直线的交点，我们采取“投票”（vote）的方法，即累加：n条直线的交点，改点的值为n；

4、遍历k-b空间，寻找出先局部最大值（极值）的点，这些点的坐标（k，b）就是图像中可能出线的直线的斜率和截距；

　　为了容易理解，这里采用了直线的斜截表达法。

　　事实上这种方法并不使用，因为某些直线的斜率很大的甚至不存在。

　　实际操作中，检测直线的霍夫变换使用含极坐标参数的直线表示型式，简称极坐标式（不是极坐标方程，因为还是在笛卡尔坐标下表示）

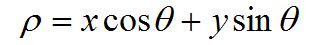
其中的两个参数的意义如下图：

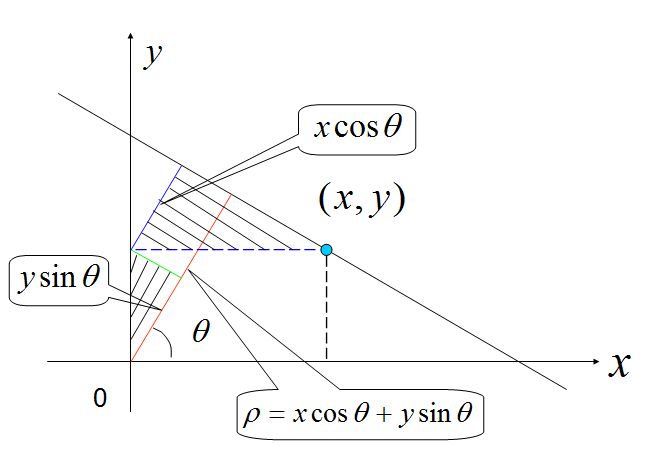
这样，每条直线对应于theta-p空间下的一条正弦曲线，同样采用投票求极值的方法寻找曲线

霍夫变换直线检测的matlab实现：

这里涉及到三个函数：hough,houghpeaks,houghlines：

1、[H,T,R] = hough(BW,'Theta',20:0.1:75)　　　　; （输入二值图像BW，角度范围与步进（最大，[-90, 90)）,返回 H-霍夫空间，T-theta，R-p)；

2、PEAKS = houghpeaks(H,NUMPEAKS)　　　　　　;（输入霍夫空间和极值数量，返回极值的坐标）

3、LINES=houghlines(BW,T,R,Peaks)　　　　　　　　; （返回lines是一个包含图像中线段首末点、p、theta的结构体）

代码：

I=imread('1.jpg');

Ihsv=rgb2hsv(I);
Iv=Ihsv(:,:,);                    %提取v空间
Ivl=Iv(:end,:);              %截取下半部
Iedge=edge(Ivl,'sobel');    %边沿检测
Iedge = imdilate(Iedge,ones());%图像膨胀

%新建窗口，绘图用
figure ()
imshow(Iedge);
hold on

%左方直线检测与绘制
%得到霍夫空间
[H1,T1,R1] = hough(Iedge,'Theta',:0.1:);
%求极值点
Peaks=houghpeaks(H1,);
%得到线段信息
lines=houghlines(Iedge,T1,R1,Peaks);
%绘制线段
 for k=:length(lines)
xy=[lines(k).point1;lines(k).point2];
plot(xy(:,),xy(:,),'LineWidth',);
 end

 %右方直线检测与绘制
[H2,T2,R2] = hough(Iedge,'Theta',-:0.1:-);
Peaks1=houghpeaks(H2,);
lines1=houghlines(Iedge,T2,R2,Peaks1);
for k=:length(lines1)
xy1=[lines1(k).point1;lines1(k).point2];
plot(xy1(:,),xy1(:,),'LineWidth',);
end

hold off

　　输入图像：

　　输出图像：

　　　　嘛，结果还是令人满意的嘛~

　　　　接下来要准备考试了，7月11号考完，之后想做一个手部识别，所以可能会玩玩haar特征检测器和光流法跟踪，大概就这样。