分组依据(Project)
《Project2016 企业项目管理实践》张会斌 董方好 编著
【视图】选项卡下,【筛选器】楼下,住着个【分组依据】。
这个功能,说白了,就是指定个“组”,把同一组的聚到一起,方便查看。如下图,左边是没分组的,同样的内容,按【资源类型】分个组,长相就变了。

下拉选项里的不够用,还可以打开【其他组】对话框,从中选择。

还不够用?那就【新建分组依据】自定义一个呗。
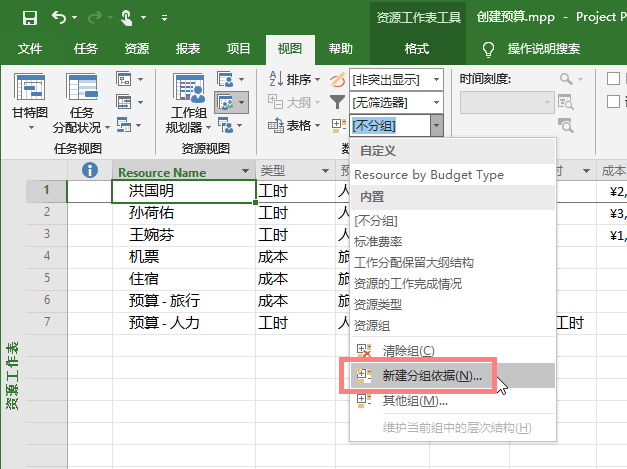
【名称】默认是“组”,最好是改成与内容匹配的;再选取【分组依据】的【域名】,从【域名】下拦选项中选择就可以,“域名”两个字,说得这么专业,其实就任务工作表的标题行;其他的,默认就可以了。分组还可以分层次,第一层是【分组依据】,接下去是各【然后依据】,一共可以分十层,够用了吧。
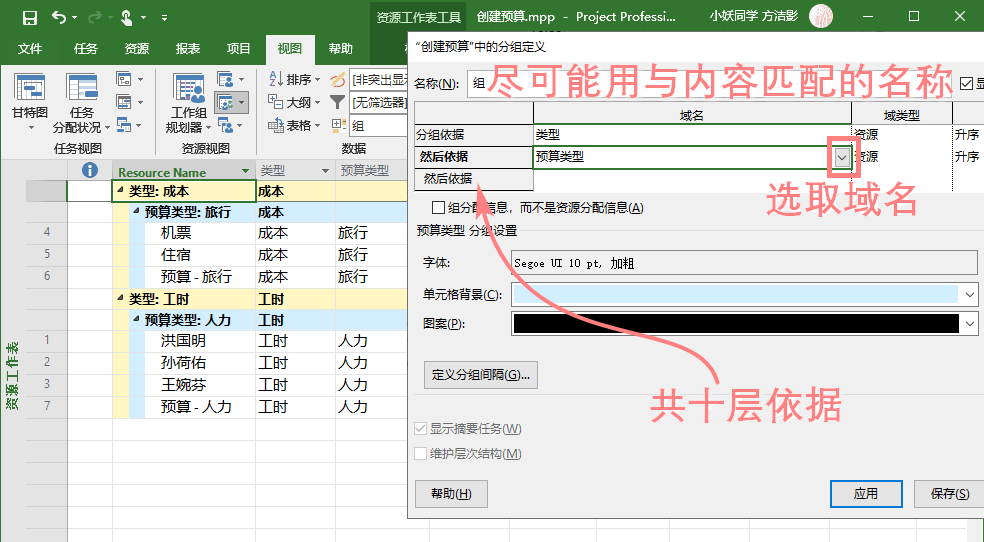
需要修改,就到【其他组】里,选上自定义的那个组以后,【编辑】一下啦。
至于怎么取消?图1-3上都有,自己找,嘿嘿~
分组依据(Project)的更多相关文章
- Informatica 常用组件Aggregator之二 分组依据端口
聚合转换允许您为聚合定义组,而不是在所有的输入数据间执行聚合.例如,您可以查找按地区分组的总销量,而不是查找总的公司销量. 要为聚合表达式定义组,请选择聚合转换中的相应输入.输入/输出.输出和变量端口 ...
- List集合分组依据集合中对象的属性
直接上代码 用到了Spring的BeanWrapper类 public static <T, K> Map<K, List<T>> groupByProperty( ...
- 与你一起学习MS Project——基础篇:Project基础应用
为了更清晰容易地熟悉掌握Project的基础应用,我们在基础篇中一起来学习掌握在Project中如何做进度计划.资源计划.成本计划以及跟踪项目的执行情况并生成所需的项目报表. 一.进度计划 这里,首先 ...
- Rdlc报表 数据汇总分组展示
1.从工具箱拉出表或者矩阵(本次使用的是矩阵) 2.选择需要的数据集,没有就新建一个数据集,名称自己起好,下面有用到 3.将行组和行列显示出来(右击报表--试图=>) 4.双击行组下的RowGr ...
- Java集合分组
public class Data { private Long id ; private Long courseId ; private String content ; public Long g ...
- WPF:ListView 分组合并
CollectionViewSource 绑定的是从数据库取出的数据ListBind 以DeptName为分组依据 <Window.Resources> <CollectionVie ...
- RDLC报表系列--------行分组报表
报表分组开发步骤: 先看总体效果:如图 下面就做个看看... 1.先将数据处理成如下结构 如图 2.创建数据集DataSet.xsd,创建表->右键选择添加数据表->添加行(ctrl+L ...
- sql server 分组统计数据
说明:group by是sql中对数据表中的数据进行分组的,在select列表中出现的字段必须全部出现在group by 字段中,出现在聚合函数中的字段在group by中可有可无,没有出现在sele ...
- MySQL最常用分组聚合函数
一.聚合函数(aggregation function)---也就是组函数 在一个行的集合(一组行)上进行操作,对每个组给一个结果. 常用的组函数: AVG([distinct] expr) 求平均值 ...
随机推荐
- [cf1209E]Rotate Columns
题意也可以理解为这样一个过程: 对于每一列,将其旋转后选出若干行上的数,要求与之前的行都不同 用$g_{i,S}$表示第$i$列选出的行数集合为$S$的最大和,$f_{i,S}$表示前$i$列$S$中 ...
- [bzoj5294]二进制
首先可以发现$2^k$模3意义下有循环节,也就是1,-1,1,-1--考虑对于x个1,y个0,判断是否存在3的倍数1.x为偶数时一定可以,选择等量的1和-1即可2.x为奇数,要满足$x\ge 3$且$ ...
- [bzoj4650]优秀的拆分
由于字符串是AABB的形式,枚举AA和BB中间的位置,分别考虑AA和BB的数量,乘起来sigma一下即为答案以下考虑AA的情况(BB同理),枚举A的长度,然后按照这个长度分为若干块,那么每一个A一定可 ...
- c语言是如何解析表达式语句"2+3*4;"的?
1. 要编译的测试代码: int main(void) { 2+3*4; } 2. 词法分析 词法分析将字符变成token,其中很重要的是token的类型,如字符2的token类型为TK_NUM,这 ...
- Docker极简入门:使用Docker运行Java程序
运行简单的Java程序 先在当前目录创建App.java文件 public class App{ public static void main(String[] args){ String os = ...
- CF 585 E Present for Vitalik the Philatelist
CF 585 E Present for Vitalik the Philatelist 我们假设 $ f(x) $ 表示与 $ x $ 互质的数的个数,$ s(x) $ 为 gcd 为 $ x $ ...
- Codeforces 306D - Polygon(随机化+乱搞)
Codeforces 题目传送门 & 洛谷题目传送门 中考终于结束了--简单写道题恢复下状态罢. 首先这一类题目肯定没法用一般的方法解决,因此考虑用一些奇淫的乱搞做法解决这道题,不难发现,如果 ...
- YAOI Round #1 (Div.2) 题解
总体来说很有一定区分度的(主要分为 4 题.2 题.1 题几档),ACM 赛制也挺有意思的,征求一下大家对这场比赛的意见吧,可以在这个帖子下回复,我都会看的. 简要题解:( A. 云之彼端,约定的地方 ...
- R语言与医学统计图形【1】par函数
张铁军,陈兴栋等 著 R语言基础绘图系统 基础绘图包之高级绘图函数--par函数 基础绘图包并非指单独某个包,而是由几个R包联合起来的一个联盟,比如graphics.grDevices等. 掌握par ...
- docker 使用加速器下载
因为docker官网的镜像地址docker.hum.com是在国外的 所以下载速度比较慢,国内有一些镜像源是比较快的,内容是和docker官网的一致 常用的加速器有 docker-cn 阿里云加速器 ...
