机器学习——正则化方法Dropout

1 前言

• 2012年，Dropout的想法被首次提出，受人类繁衍后代时男女各一半基因进行组合产生下一代的启发，论文《Dropout: A Simple Way to Prevent Neural Networks from Overfitting》 提出了Dropout，它的出现彻底改变了深度学习进度，之后深度学习方向(反馈模型)开始展现优势，传统的机器学习慢慢消声。
• 深度学习架构现在变得越来越深，dropout 作为一个防过拟合的手段，使用也越来越普遍。

2 Dropout具体实现

• Dropout的思路：在一次循环中先随机选择神经层中的一些单元并将其临时隐藏，然后再进行该次循环中神经网络的训练和优化过程，在下一次循环中，又将隐藏另外一些神经元，如此直至训练结束。这样每次都会有一种新的组合，假设某一层有 $N$ 个神经元，就有 $2^N$ 个组合，最后子网络的输出均值就是最终的结果。但如果同时训练这些子网络代价太大，而且测试时又要组合多个网络的输出结果，不可行。

• 在训练时，每个神经单元以概率 $p$ 被保留(dropout丢弃率为$1-p$)；在测试阶段，每个神经单元都是存在的，权重参数 $w$ 要乘以 $p$，变成 $ pw$ 。测试时需要乘上 $p$ 的原因：考虑第一隐藏层的一个神经元在 dropout 之前的输出是 $x$，那么 dropout 之后的期望值是 $E=px+(1−p)0 $，在测试时该神经元总是激活，为了保持同样的输出期望值并使下一层也得到同样的结果，需要调整$x→px$. 其中 $p$ 是 Bernoulli 分布 $(0-1分布)$ 中值为 $1$ 的概率。

　　

3 Dropout具体工作流程

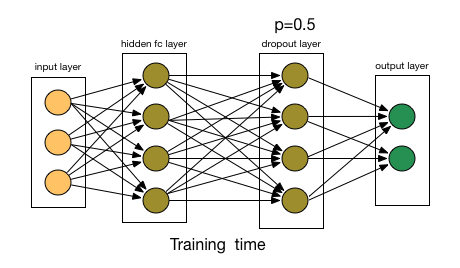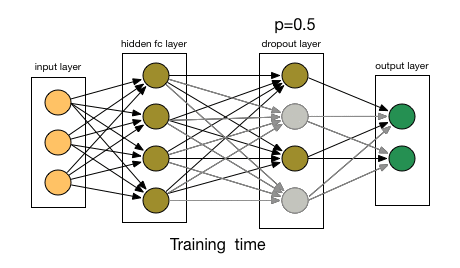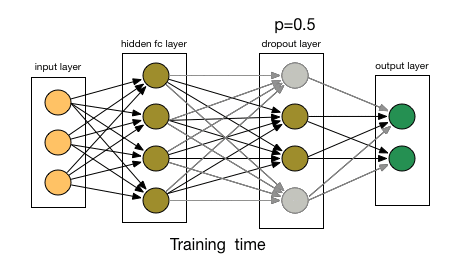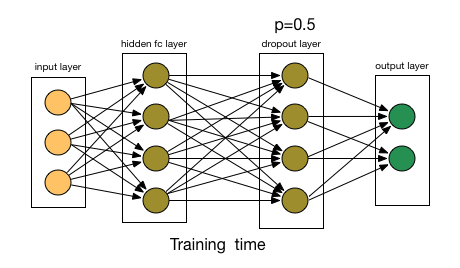
• 为了了解Dropout，假设我们的神经网络结构类似于以下所示：（这里图只有Hidden layer，Output layer）

　　

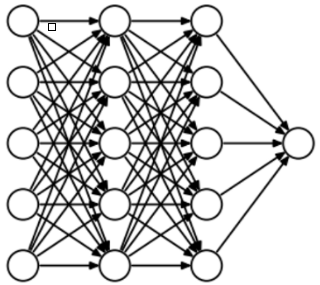
• 输入是 $x$ 输出是 $y$，正常的流程是：我们首先把 $x$ 通过网络前向传播，然后把误差反向传播以决定如何更新参数让网络进行学习。使用Dropout之后，过程变成如下：

• (1)首先随机(临时)删掉网络中一半的隐藏神经元，输入输出神经元保持不变。

　　

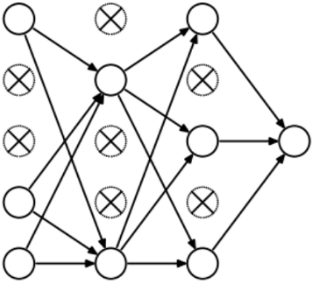
• (2)然后把输入 $x$ 通过修改后的网络前向传播，然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后，在没有被删除的神经元上按照随机梯度下降法更新对应的参数$(w，b)$。
• (3)然后继续重复这一过程：因此，每个迭代都有一组不同的节点，这会导致一组不同的输出。 也可以将其视为机器学习中的集成技术。
  • 恢复被删掉的神经元（此时被删除的神经元保持原样，而没有被删除的神经元已经有所更新）
  • 从隐藏层神经元中随机选择一个一半大小 $(ρ=0.5)$ 的子集临时删除掉(备份被删除神经元的参数)。
  • 对一小批训练样本，先前向传播然后反向传播损失并根据随机梯度下降法更新参数 $(w，b)$ (没有被删除的那一部分参数得到更新，删除的神经元参数，保持被删除前的结果)。
• Dropout也比正常的神经网络模型表现更好。选择应该删除多少个节点的这种可能性是丢失函数的超参数。 如上图所示，Dropout既可以应用于隐藏层，也可以应用于输入层。