hdu 3863 No Gambling (不会证明,但是是对的,,)
题意:
N=4时
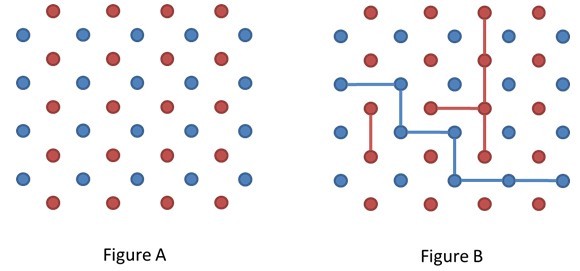
规则:
双方每次可以连接自己颜色的两个点(相邻,长度为1),线和线不能交叉重叠。
蓝方要连接左右,红方要连接上下。
蓝方先。问谁先连接?
思路:
经过观察。。。。蓝方胜。。。。。。。(无语)【我不知道如何证明!】
代码:
就不贴了。。。
hdu 3863 No Gambling (不会证明,但是是对的,,)的更多相关文章
- hdu 3863 No Gambling
#include<stdio.h> int main() { int n; ) { printf("I bet on Oregon Maple~\n"); } ; } ...
- 【hdu 3863】No Gambling
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65568/32768 K (Java/Others) Total Submission(s) ...
- HDU 3863 (博弈) No Gambling
这是我见过的最简单的一道博弈了,其实不要被复杂的棋盘吓到了. 首先肯定会有而且仅有一个人胜,而且因为棋盘是对称的,所以先手相对于后手肯定更有优势,那么肯定是先手赢. 这是不是严格的推理,但是确实比较容 ...
- acm--博弈入门2(P/N分析)--(HDU 1847 HDU 2188 HDU 3863)
P/N理论 分析博弈时可以用P/N分析法 具体如下: P点:即必败点,某玩家位于此点,只要对方无失误,则必败: N点:即必胜点,某玩家位于此点,只要自己无失误,则必胜. 必败态:一定输 必胜态:一定赢 ...
- 有向图 加最少的边 成为强连通分量的证明 poj 1236 hdu 2767
poj 1236: 题目大意:给出一个有向图, 任务一: 求最少的点,使得从这些点出发可以遍历整张图 任务二: 求最少加多少边 使整个图变成一个强连通分量. 首先任务一很好做, 只要缩点 之后 求 ...
- Girls and Boys HDU - 1068 二分图匹配(匈牙利)+最大独立集证明
最大独立集证明参考:https://blog.csdn.net/qq_34564984/article/details/52778763 最大独立集证明: 上图,我们用两个红色的点覆盖了所有边.我们证 ...
- 有向图最小路径覆盖方法浅析、证明 //hdu 3861
路径覆盖就是在图中找一些路径,使之覆盖了图中的所有顶点,且任何一个顶点有且只有一条路径与之关联. 对于一个有向无环图怎么求最小路径覆盖? 先构造二分图: 对于原图,先拆点,吧每个点i拆成ii,iii. ...
- HDU 4923 (贪心+证明)
Room and Moor Problem Description PM Room defines a sequence A = {A1, A2,..., AN}, each of which is ...
- 【Mark】博弈类题目小结(HDU,POJ,ZOJ)
转载请注明出处,谢谢http://blog.csdn.net/ACM_cxlove?viewmode=contents by---cxlove 首先当然要献上一些非常好的学习资料: 基础博弈的小 ...
随机推荐
- CodeForce-811B Vladik and Complicated Book(水题)
http://codeforces.com/problemset/problem/811/B 题意: 给定一个长度为 N 不重复的数字序列,然后对其进行 M 次询问. 每次询问含L,R,X三个值,问如 ...
- Docker安装flink及避坑指南
Docker安装flink 导航 无处不在的大数据 安装flink 拉取flink镜像 编写docker-compose.yml 生成启动 查看安装效果 常见坑及解决方案 问题1 问题2 参考 本 ...
- php超时报错: Maximum execution time of 300 seconds exceeded
php.ini里max_execution_time = 30,原因是这个脚本执行时间太小了,增加一些,或者改成0不限制 可以增加代码: set_time_limit(0);
- 自学 Java开发(Java后台开发|Java后端开发)的书籍推荐
java编程思想java并发编程实战深入理解java虚拟机函数式编程思维tcp/ip详解鸟哥的linux私房菜spring mvc +mybatis开发从入门到精通spring技术内幕elastics ...
- 使用jacob调用Windows的com对象,进行word、ppt等转换成ptf、html(二)
富文本转pdf : 注意:simsun.ttc 可以百度下载:http://www.pc6.com/softview/SoftView_100415.html package com.orangecd ...
- PYTHON django 关于时间转换
在安装django.默认会pytz时区库,import pytzpytz.timezone("UTC")now.astimezone("要转换的aware类型" ...
- kettle 多表全删全插同步数据 两种方案
背景: 接到上级指示,要从外网某库把数据全部导入到内网,数据每天更新一次即可,大约几百万条数据,两个库结构一样,mysql的,两台数据库所在服务器都是windows server的,写个java接口实 ...
- Dubbo管理平台搭建(duboo-admin-2.5.4)遇到的问题:org.springframework.beans.factory.BeanCreationException: Error creating bean with name 'uriBrokerService': Cannot create inner bean '(inner bean)' of type
1.将dubbo的war包方式tomcat的webapps文件夹下,启动tomcat报错 错误信息如下: ERROR context.ContextLoader - Context initializ ...
- mybatis-plus最新版代码生成器(Swagger3)
写项目想用mybatis-plus+swagger3,百度最新版代码生成器都是旧版的,且官网的配置过于简洁,所以手敲一份,在官网的基础上加了一堆配置,lombok,restful,mvc三层结构目录等 ...
- 阿里云服务器上在docker部署jenkins
1.查询jenkins:docker search jenkins 2.拉取jenkins镜像 docker pull jenkins/jenkins:lts 3.新建jenkins的工作目录: mk ...
