时序分解算法：STL

1. 详解

STL (Seasonal-Trend decomposition procedure based on Loess) [1] 为时序分解中一种常见的算法，基于LOESS将某时刻的数据\(Y_v\)分解为趋势分量（trend component）、周期分量（seasonal component）和余项（remainder component）:

\[Y_v = T _v + S_v + R_v \quad v= 1, \cdots, N
\]

STL分为内循环（inner loop）与外循环（outer loop），其中内循环主要做了趋势拟合与周期分量的计算。假定\(T_v^{(k)}\)、\(S_v{(k)}\)为内循环中第k-1次pass结束时的趋势分量、周期分量，初始时\(T_v^{(k)} = 0\)；并有以下参数：

• \(n_{(i)}\)内层循环数，
• \(n_{(o)}\)外层循环数，
• \(n_{(p)}\)为一个周期的样本数，
• \(n_{(s)}\)为Step 2中LOESS平滑参数，
• \(n_{(l)}\)为Step 3中LOESS平滑参数，
• \(n_{(t)}\)为Step 6中LOESS平滑参数。

每个周期相同位置的样本点组成一个子序列（subseries），容易知道这样的子序列共有共有\(n_(p)\)个，我们称其为cycle-subseries。内循环主要分为以下6个步骤：

• Step 1: 去趋势（Detrending），减去上一轮结果的趋势分量，\(Y_v - T_v^{(k)}\)；
• Step 2: 周期子序列平滑（Cycle-subseries smoothing），用LOESS (\(q=n_{n(s)}\), \(d=1\))对每个子序列做回归，并向前向后各延展一个周期；平滑结果组成temporary seasonal series，记为$C_v^{(k+1)}, \quad v = -n_{(p)} + 1, \cdots, -N + n_{(p)} $；
• Step 3: 周期子序列的低通量过滤（Low-Pass Filtering），对上一个步骤的结果序列\(C_v^{(k+1)}\)依次做长度为\(n_(p)\)、\(n_(p)\)、\(3\)的滑动平均（moving average），然后做LOESS (\(q=n_{n(l)}\), \(d=1\))回归，得到结果序列\(L_v^{(k+1)}, \quad v = 1, \cdots, N\)；相当于提取周期子序列的低通量；
• Step 4: 去除平滑周期子序列趋势（Detrending of Smoothed Cycle-subseries），\(S_v^{(k+1)} = C_v^{(k+1)} - L_v^{(k+1)}\)；
• Step 5: 去周期（Deseasonalizing），减去周期分量，\(Y_v - S_v^{(k+1)}\)；
• Step 6: 趋势平滑（Trend Smoothing），对于去除周期之后的序列做LOESS (\(q=n_{n(t)}\), \(d=1\))回归，得到趋势分量\(T_v^{(k+1)}\)。

外层循环主要用于调节robustness weight。如果数据序列中有outlier，则余项会较大。定义

\[h = 6 * median(|R_v|)
\]

对于位置为\(v\)的数据点，其robustness weight为

\[\rho_v = B(|R_v|/h)
\]

其中\(B\)函数为bisquare函数：

\[B(u) = \left \{
{
\matrix {
{(1-u^2)^2 } & {for \quad 0 \le u < 1} \cr
{ 0} & {for \quad u \ge 1} \cr
}
}
\right.
\]

然后每一次迭代的内循环中，在Step 2与Step 6中做LOESS回归时，邻域权重（neighborhood weight）需要乘以\(\rho_v\)，以减少outlier对回归的影响。STL的具体流程如下：

outer loop:
	计算robustness weight;
	inner loop:
		Step 1 去趋势;
		Step 2 周期子序列平滑;
		Step 3 周期子序列的低通量过滤;
		Step 4 去除平滑周期子序列趋势;
		Step 5 去周期;
		Step 6 趋势平滑;

为了使得算法具有足够的robustness，所以设计了内循环与外循环。特别地，当\(n_{(i)}\)足够大时，内循环结束时趋势分量与周期分量已收敛；若时序数据中没有明显的outlier，可以将\(n_{(o)}\)设为0。

R提供STL函数，底层为作者Cleveland的Fortran实现。Python的statsmodels实现了一个简单版的时序分解，通过加权滑动平均提取趋势分量，然后对cycle-subseries每个时间点数据求平均组成周期分量：

def seasonal_decompose(x, model="additive", filt=None, freq=None, two_sided=True):
	_pandas_wrapper, pfreq = _maybe_get_pandas_wrapper_freq(x)
    x = np.asanyarray(x).squeeze()
    nobs = len(x)
    ...
    if filt is None:
      if freq % 2 == 0:  # split weights at ends
        filt = np.array([.5] + [1] * (freq - 1) + [.5]) / freq
        else:
          filt = np.repeat(1./freq, freq)

    nsides = int(two_sided) + 1
    # Linear filtering via convolution. Centered and backward displaced moving weighted average.
    trend = convolution_filter(x, filt, nsides)
    if model.startswith('m'):
        detrended = x / trend
    else:
        detrended = x - trend

    period_averages = seasonal_mean(detrended, freq)

    if model.startswith('m'):
        period_averages /= np.mean(period_averages)
    else:
        period_averages -= np.mean(period_averages)

    seasonal = np.tile(period_averages, nobs // freq + 1)[:nobs]

    if model.startswith('m'):
        resid = x / seasonal / trend
    else:
        resid = detrended - seasonal

    results = lmap(_pandas_wrapper, [seasonal, trend, resid, x])
    return DecomposeResult(seasonal=results[0], trend=results[1],
                           resid=results[2], observed=results[3])

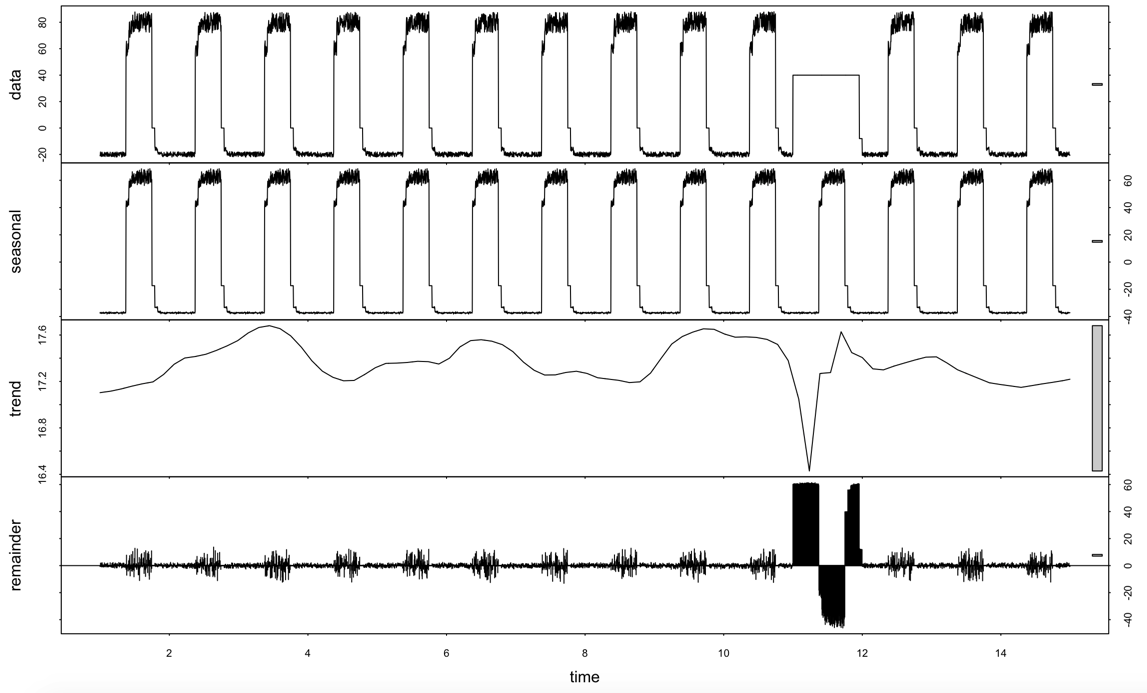
R版STL分解带噪音点数据的结果如下图：

data = read.csv("artificialWithAnomaly/art_daily_flatmiddle.csv")
View(data)
data_decomp <- stl(ts(data[[2]], frequency = 1440/5), s.window = "periodic", robust = TRUE)
plot(data_decomp)

statsmodels模块的时序分解的结果如下图：

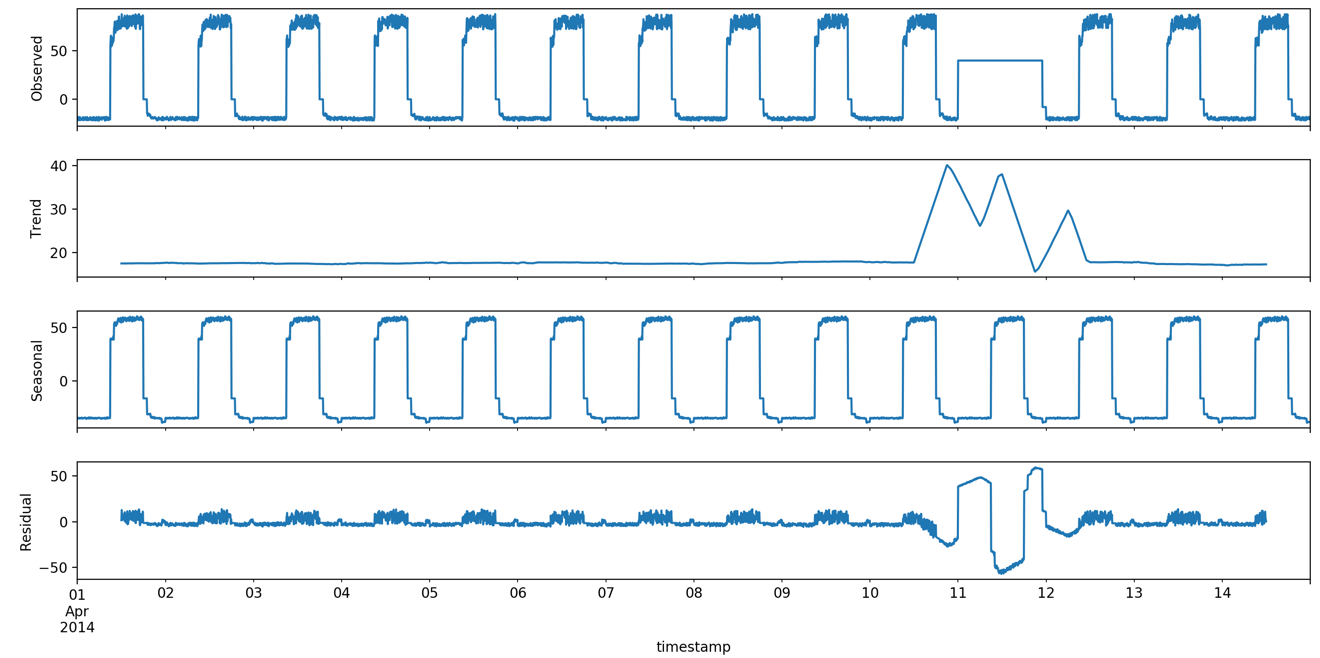
import statsmodels.api as sm
import matplotlib.pyplot as plt
import pandas as pd
from date_utils import get_gran, format_timestamp

dta = pd.read_csv('artificialWithAnomaly/art_daily_flatmiddle.csv',
                                   usecols=['timestamp', 'value'])
dta = format_timestamp(dta)
dta = dta.set_index('timestamp')
dta['value'] = dta['value'].apply(pd.to_numeric, errors='ignore')
dta.value.interpolate(inplace=True)
res = sm.tsa.seasonal_decompose(dta.value, freq=288)
res.plot()
plt.show()

2. 参考资料

[1] Cleveland, Robert B., William S. Cleveland, and Irma Terpenning. "STL: A seasonal-trend decomposition procedure based on loess." Journal of Official Statistics 6.1 (1990): 3.