POJ 3128 Leonardo's Notebook （置换）

Leonardo's Notebook

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 2324		Accepted: 988

Description

— I just bought Leonardo's secret notebook! Rare object collector Stan Ucker was really agitated but his friend, special investigator Sarah Kepticwas unimpressed. 
— How do you know it is genuine? 
— Oh, it must be, at that price. And it is written in the da Vinci code. Sarah browsed a few of the pages. It was obvious to her that the code was a substitution cipher, where each letter of the alphabet had been substituted by another letter. 
— Leonardo would have written the plain-text and left it to his assistant to encrypt, she said. And he must have supplied the substitution alphabet to be used. If we are lucky, we can find it on the back cover! She turned up the last page and, lo and behold, there was a single line of all 26 letters of the alphabet: 
QWERTYUIOPASDFGHJKLZXCVBNM 
— This may be Leonardo's instructions meaning that each A in the plain-text was to be replaced by Q, each B withW, etcetera. Let us see... To their disappointment, they soon saw that this could not be the substitution that was used in the book. Suddenly, Stan brightened. 
— Maybe Leonardo really wrote the substitution alphabet on the last page, and by mistake his assistant coded that line as he had coded the rest of the book. So the line we have here is the result of applying some permutation TWICE to the ordinary alphabet! Sarah took out her laptop computer and coded fiercely for a few minutes. Then she turned to Stan with a sympathetic expression. 
— No, that couldn't be it. I am afraid that you have been duped again, my friend. In all probability, the book is a fake.

Write a program that takes a permutation of the English alphabet as input and decides if it may be the result of performing some permutation twice.

Input

The input begins with a positive number on a line of its own telling the number of test cases (at most 500). Then for each test case there is one line containing a permutation of the 26 capital letters of the English alphabet.

Output

For each test case, output one line containing Yes if the given permutation can result from applying some permutation twice on the original alphabet string ABC...XYZ, otherwise output No.

Sample Input

2
QWERTYUIOPASDFGHJKLZXCVBNM
ABCDEFGHIJKLMNOPQRSTUVWXYZ

Sample Output

No
Yes

Source

题意：

　　给你一串大写的英文字母， 问你能不能通过2次置换ABCD···XYZ使得变成你要的字母串。

题解：

　　如果存在一个置换 （a1, a2, a3）。那么 （a1, a2, a3）（a1, a2, a3） = （a1， a3， a2）。

　　如果存在一个置换（b1, b2, b3, b4）。那么 （b1, b2, b3, b4）（b1, b2, b3, b4） = （b1, b3）（b2, b4）

　　证明：

（a1, a2, a3）表示的是 a1 -> a2 , a2 -> a3 , a3 -> a1。

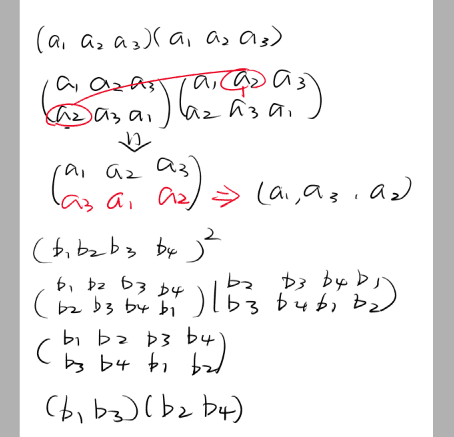
（需要学习置换的乘法）

当任意两个长度为n（奇数）的置换，都可以找到一个置换A ， 满足A^2 = B。

当任意两个不相交的长度为n（奇数偶数都可以）循环置换 B, C ，都能找到一个长度为2n的循环置换A， 满足 A^2 = B C。

所以只要长度为偶数的置换有偶数个就可以输出Yes。

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <string>
 #include <algorithm>
 #include <cmath>
 #include <vector>
 #include <queue>
 #include <stack>
 #include <set>
 using namespace std;
 typedef long long LL;
 #define ms(a, b) memset(a, b, sizeof(a))
 #define pb push_back
 #define mp make_pair
 const int INF = 0x7fffffff;
 const int inf = 0x3f3f3f3f;
 const int mod = 1e9+;
 const int maxn = +;
 void init(){

 }
 void solve() {
     char B[];
     int vis[], cnt[], T;
     scanf("%d", &T);
     while(T--){
         scanf("%s", B);
         ms(vis, );
         ms(cnt, );
         for(int i = ;i<;i++){
             if(!vis[i]){
                 int j = i, n = ;
                 //cnt为长度
                 do{
                     vis[j] = ;
                     j = B[j] - 'A';
                     n++;
                 }while(j!=i);
                 cnt[n]++;
             }
         }
         int ok = ;
         for(int i = ;i<=;i+=)
             if(cnt[i]%==)
                 ok = ;
         if(ok)  printf("Yes\n");
         else    printf("No\n");
     }
 }
 int main() {
 #ifdef LOCAL
     freopen("input.txt", "r", stdin);
 //        freopen("output.txt", "w", stdout);
 #endif
     ios::sync_with_stdio();
     cin.tie();
     init();
     solve();
     return ;
 }