【例题收藏】◇例题·I◇ Snuke's Subway Trip

◇例题·I◇ Snuke's Subway Trip

题目来源：Atcoder Regular 061 E题（beta版） +传送门+

---

一、解析

（1）最短路实现

由于在同一家公司的铁路上移动是不花费的，只有在换乘时会花费1日元。我们可以视换乘的花费为点权——当换乘到不同公司时花费1，同一家公司时花费0。

对于这种点权因情况而变化的题，最常见的做法便是拆点。设节点 u 相连的铁路由 c₁，c₂，...，c_p p个公司修建，则将节点u拆分为节点 u_c1~u_cp，点u_ci表示到达点u的铁路是由公司c_i修建的。若两点u,v被公司c修的铁路相连，则将 u_c 与 v_c 连接一条权为0的边——因为在同一家公司的铁路上移动无花费。

举个例子：

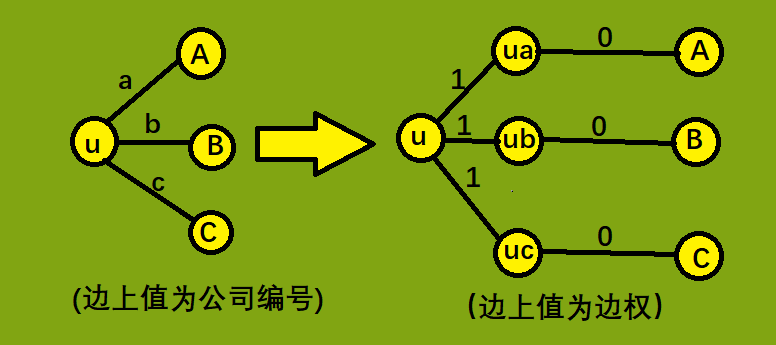
拆完点后SPFA跑一次最短路，最后答案要除以2。

为什么可以这样做呢？

如果只通过公司c的铁路能够从u到v（中途不转到其他公司的铁路），那么我们就能够从u_c花费0日元移动到v_c。

如果在节点u要从a公司转到b公司，我们需要通过 u_a->u->u_b。如何理解这一过程呢？我们可以把u看成一个站点——你到达u时在公司a的站台上，然后你需要花费1日元回到站点u，然后通过站点u中转，再花费1日元到达公司b的站台。但是我们会发现，题目要求是换乘只需要1日元，而我的程序每换乘一次需要2日元，就会比正确答案大一倍，所以最后要除以2。

可能不太清楚，看个例子

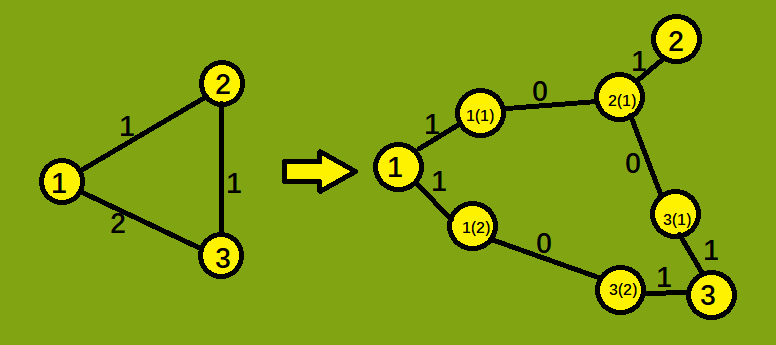
（我觉得我好像讲的不大清楚，reader们不懂的可以看文章底的邮箱问我 QwQ）

(2) 二分图实现

（其实我这种实现写TLE了……但是我知道有这种思路，于是写上了）

对于原图，我们定义可以通过同一家公司的铁路到达的点集为一个连通块，也就是说在同一个连通块内的所有点互相可以到达，且经过的铁路是同一家公司的（花费为0），而不同的连通块的点互相到达需要花费。

由于一个连通块的点之间花费为0，我们可以把每个连通块都缩成一个点x，把该连通块内的点与x连接。然后我们会发现这样构成的图形成了一个二分图，X部为原图的点，Y部为连通块缩成的点。再用BFS从原图的点1（起点）到原图的点n（终点）搜索一遍求得1到n的最短路，把所得解除以2就是答案。

（同样的问题）为什么可以这么做呢？

可以把X部看成中转站，而Y部为铁路。因为连通块内的点可以互相到达，我们把从中转站进入铁路的花费和从铁路出到中转站的花费都设为1，那么同一个连通块内的两个点u,v的最小花费路径则是从u出发经过连通块内的其他点到达v，花费为0。同样，从点1到点n的路径可以看成从1出发经过若干个连通块到达n。我们可以证明——从1到n的最短路径经过同一个连通块的次数不超过1——设最短路径进入某一个连通块时点为u，而从该连通块离开的点为v，一定存在一条花费为0的从u到v的路径（因为他们在一个连通块内嘛），而如果从u出发，经过其他连通块再到达v，则花费一定大于0，因此经过该连通块的次数一定不超过1。

其实不难发现，u到v的最小花费就是u到v的最短路径中经过的连通块的个数（看下面的例子），而且u到v的路径在二分图中一定是“u->连通块1->中转站1->...->中转站k->连通块k->v（k就是答案）”，在二分图中形成k个“V”形，即经过边数为 2k 条。所以答案（k）就是经过边数除以2。

---

二、实现

就只讲一下那些比较难写的地方，简单的步骤就默认大家会了……

（1）最短路拆点 - map储存编号(ID)

这一步可以在线处理。对于点u储存一个map<int,int>ID[u]，ID[u][c]表示u的由c公司修的铁路所拆分的虚拟节点的编号。可以在读入边的时候处理——用map自带的函数count(c)判断端点u,v的映射（map）中是否存在公司c，如果没有，则给它赋一个值cnt。我们可以把虚拟节点的编号储存在原图节点的后面，即cnt从n+1开始。同时连接u,v关于c公司生成的两个虚拟节点 ID[u][c],ID[v][c]。

再枚举1~n的点，对于每一个点i，用迭代器枚举map。这里是一个技巧，大家可以看一看：

迭代器iterator——STL容器遍历利器

迭代器相当于一个指针，可以指向特定STL容器的元素。由于STL容器除了vector好像就没有可以直接访问、遍历元素（在不改变原容器的情况下）的容器了，遍历起来就比较麻烦。我们可以定义一个迭代器，map的格式就像这样 “map<类型,类型>::iterator”。迭代器本身是一个数据类型，若要遍历一个 map<int,int> ma ，迭代器就定义为 "map<int,int>::iterator it"，用for循环枚举：“for(map<int,int>::iterator it=ma.begin();it!=ma.end();it++)” 。这里的"it++"是迭代器重定义了"++"，指向容器的下一个元素。

map<>这种容器比较特别，它的元素其实是一个pair，其中pair的first是下标，second是下标对应的值。注意用迭代器访问元素时，迭代器类似于指针，所以访问first,second时是用指针的"->"而不是结构体的"."。

这里的second就是该虚拟节点对应的ID，直接将该虚拟节点与节点i连边即可。

for(int i=;i<n_edg;i++)
{
    int u,v,c;scanf("%d%d%d",&u,&v,&c); //读边
    input[i][]=u;input[i][]=v;input[i][]=c;
    if(!ID[u].count(c)) ID[u][c]=cnt++; //存虚拟节点id
    if(!ID[v].count(c)) ID[v][c]=cnt++;
    lnk[ID[u][c]].push_back(make_pair(ID[v][c],)); //连接两个虚拟节点
    lnk[ID[v][c]].push_back(make_pair(ID[u][c],));
}
for(int i=;i<=n_pnt;i++) //枚举原图点
    for(map<int,int>::iterator it=ID[i].begin();it!=ID[i].end();it++) //枚举虚拟点
    {
        int id=it->second; //id是虚拟节点的编号
        lnk[i].push_back(make_pair(id,)); //连接原图点与虚拟节点
        lnk[id].push_back(make_pair(i,));
    }

（2）二分图改造 - 原图与二分图的转换（我觉得就是这里TLE了）

先用vector<>邻接表储存原图 fir_lnk，再用map<int,bool> cpn[]，cpn[u][k]表示与节点u连接的铁路是否有k公司修的，即属于公司k的铁路连通块是否包含u。

枚举点 1~n，再用迭代器枚举公司，如果节点 i 与公司 j 的连通块还没有被枚举到，则用 BFS(Linker) 遍历该连通块，遍历到一个点后清除该点与连通块的标记，同时连接点与连通块（构造二分图）。

Linker:

void Linker(int start,int edge,int ID)
{
    queue<int> que;
    que.push(start);
    while(!que.empty())
    {
        int u=que.front();que.pop();
        lnk[u].push_back(ID); //构造二分图
        lnk[ID].push_back(u);
        for(int i=;i<fir_lnk[u].size();i++)
            if(fir_lnk[u][i].second==edge)
            {
                int v=fir_lnk[u][i].first;
                if(!cpn[v][edge]) continue;
                cpn[v][edge]=false; //清除标记
                que.push(v);
            }
    }
}

枚举：

for(int i=;i<=n_pnt;i++) //枚举点
    for(map<int,bool>::iterator it=cpn[i].begin();it!=cpn[i].end();it++) //枚举连通块
        if(it->second)
            Linker(i,it->first,cnt++); //BFS

---

三、源代码

（最短路 AC）

 /*Lucky_Glass*/
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<iostream>
 #include<map>
 #include<vector>
 #include<queue>
 using namespace std;
 const int MAXN=(int)1e5;
 const int INF=(int)1e9;
 int n_pnt,n_edg,cnt;
 map<int,int> ID[MAXN+];
 int input[*MAXN+][];
 vector<pair<int,int> > lnk[*MAXN+];
 int dist[*MAXN+];
 bool vis[*MAXN+];
 int main()
 {
     scanf("%d%d",&n_pnt,&n_edg);
     cnt=n_pnt+;
     for(int i=;i<n_edg;i++)
     {
         int u,v,c;scanf("%d%d%d",&u,&v,&c);
         input[i][]=u;input[i][]=v;input[i][]=c;
         if(!ID[u].count(c)) ID[u][c]=cnt++;
         if(!ID[v].count(c)) ID[v][c]=cnt++;
         lnk[ID[u][c]].push_back(make_pair(ID[v][c],));
         lnk[ID[v][c]].push_back(make_pair(ID[u][c],));
     }
     for(int i=;i<=n_pnt;i++)
         for(map<int,int>::iterator it=ID[i].begin();it!=ID[i].end();it++)
         {
             int id=it->second;
             lnk[i].push_back(make_pair(id,));
             lnk[id].push_back(make_pair(i,));
         }
     fill(dist,dist+*MAXN+,INF);
     dist[]=;vis[]=true;
     queue<int> que;que.push();
     while(!que.empty())
     {
         int u=que.front();que.pop();
         for(int i=;i<lnk[u].size();i++)
         {
             int v=lnk[u][i].first,l=lnk[u][i].second;
             if(dist[v]>dist[u]+l)
             {
                 dist[v]=dist[u]+l;
                 if(!vis[v])
                     vis[v]=true,que.push(v);
             }
         }
         vis[u]=false;
     }
     if(dist[n_pnt]==INF) printf("%d\n",-);
     else printf("%d\n",dist[n_pnt]/);
     return ;
 }

（二分图 TLE）

 /*Lucky_Glass*/
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<vector>
 #include<queue>
 #include<map>
 using namespace std;
 int n_pnt,n_edg,cnt;
 const int MAXN=int(3e5);
 vector<int> lnk[MAXN+];
 vector<pair<int,int> > fir_lnk[int(1e5)+];
 map<int,bool> cpn[int(1e5)+];
 bool vis[MAXN+],fir_vis[int(1e5)+];
 void Linker(int start,int edge,int ID)
 {
     queue<int> que;
     que.push(start);
     while(!que.empty())
     {
         int u=que.front();que.pop();
         lnk[u].push_back(ID);
         lnk[ID].push_back(u);
         for(int i=;i<fir_lnk[u].size();i++)
             if(fir_lnk[u][i].second==edge)
             {
                 int v=fir_lnk[u][i].first;
                 if(!cpn[v][edge]) continue;
                 cpn[v][edge]=false;
                 que.push(v);
             }
     }
 }
 int main()
 {
     scanf("%d%d",&n_pnt,&n_edg);
     cnt=n_pnt+;
     for(int i=;i<n_edg;i++)
     {
         int u,v,c;
         scanf("%d%d%d",&u,&v,&c);
         fir_lnk[u].push_back(make_pair(v,c));
         fir_lnk[v].push_back(make_pair(u,c));
         cpn[u][c]=cpn[v][c]=true;
     }
     for(int i=;i<=n_pnt;i++)
         for(map<int,bool>::iterator it=cpn[i].begin();it!=cpn[i].end();it++)
             if(it->second)
                 Linker(i,it->first,cnt++);
     queue<pair<int,int> > que;
     que.push(make_pair(,));
     while(!que.empty())
     {
         pair<int,int> fro=que.front();que.pop();
         int u=fro.first,stp=fro.second;
         for(int i=;i<lnk[u].size();i++)
         {
             int v=lnk[u][i],fstp=stp+;
             if(vis[v]) continue;
             vis[v]=true;
             if(v==n_pnt) {printf("%d\n",fstp/);return ;}
             que.push(make_pair(v,fstp));
         }
     }
     printf("-1\n");
     return ;
 }

---

The End

Thanks for reading!

- Lucky_Glass

（Tab：如果我有没讲清楚的地方可以直接在邮箱lucky_glass@foxmail.com email我，在周末我会尽量解答并完善博客~）