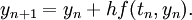Euler-Maruyama discretization("欧拉-丸山"数值解法)

欧拉法的来源
在数学和计算机科学中,欧拉方法(Euler method)命名自它的发明者莱昂哈德·欧拉,是一种一阶数值方法,用以对给定初值的常微分方程(即初值问题)求解。它是一种解决常微分方程数值积分的最基本的一类显型方法(Explicit method)。
什么是欧拉法
欧拉法是以流体质点流经流场中各空间点的运动即以流场作为描述对象研究流动的方法。——流场法
它不直接追究质点的运动过程,而是以充满运动液体质点的空间——流场为对象。研究各时刻质点在流场中的变化规律。将个别流体质点运动过程置之不理,而固守于流场各空间点。通过观察在流动空间中的每一个空间点上运动要素随时间的变化,把足够多的空间点综合起来而得出的整个流体的运动情况。
常微分方程的数值解法的一种。基本思想是迭代。其中分为前进的EULER法、后退的EULER 法、改进的EULER法。所谓迭代,就是逐次替代,最后求出所要求的解,并达到一定的精度。误差可以很容易的计算出来。
欧拉算法
微分方程的本质特征是方程中含有导数项,数值解法的第一步就是设法消除其导数值,这个过程称为离散化。实现离散化的基本途径是用向前差商来近似代替导数,这就是欧拉算法实现的依据。欧拉(Euler)算法是数值求解中最基本、最简单的方法,但其求解精度较低,一般不在工程中单独进行运算。所谓数值求解,就是求问题的解y(x)在一系列点上的值y(xi)的近似值yi。对于常微分方程:
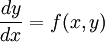 ,x∈[a,b]
,x∈[a,b]
y(a) = y0
可以将区间[a,b]分成n段,那么方程在第xi点有y'(xi) = f(xi,y(xi)),再用向前差商近似代替导数则为: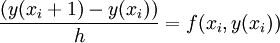 ,在这里,h是步长,即相邻两个结点间的距离。因此可以根据xi点和yi点的数值计算出yi+1来:
,在这里,h是步长,即相邻两个结点间的距离。因此可以根据xi点和yi点的数值计算出yi+1来:
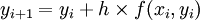 ,i=0,1,2,L
,i=0,1,2,L
这就是欧拉格式,若初值yi + 1是已知的,则可依据上式逐步算出数值解y1,y2,L。
为简化分析,人们常在yi为准确即yi = y(xi)的前提下估计误差 y(xi + 1) − yi + 1,这种误差称为局部截断误差。
如果一种数值方法的局部截断误差为O(hp + 1),则称它的精度是p阶的,或称之为p阶方法。欧拉格式的局部截断误差为O(h2),由此可知欧拉格式仅为一阶方法。
欧拉公式
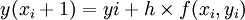
且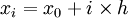 (i=0,1,2,…,n-1)
(i=0,1,2,…,n-1)
局部截断误差是O(h2)
非形式化的几何诠释
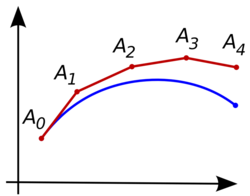
考虑计算下面一个未知曲线的形状:它具有给定的起点并且满足一个给定的微分方程。这里,所谓“微分方程”可以看作能够通过曲线上任意点的位置而计算出这一点的切线斜率的公式。
思路是,一开始只知道曲线的起点,曲线其他部份是未知的,不过通过微分方程,的斜率可以被计算出来,也就得到了切线。
顺着切线向前走一小步到点。如果我们假设是曲线上的一点(实际上通常不是),那么同样的道理就可以确定下一条切线,依此类推。在经过几步之后,一条折线就被计算出来了。大部分的情况下,这条折线与原先的未知曲线偏离不远,并且任意小的误差都可以通过减少步长来得到(虽然对于刚性方程而言会比较复杂)。
欧拉方法的推导
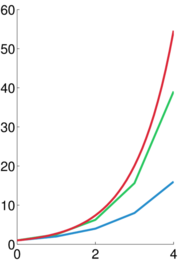
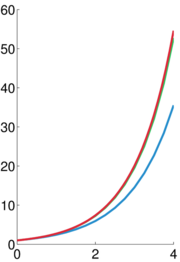
以以下微分方程为例 
希望用y 在点(t0,y(t0)) 附近的线性近似来得到其近似解。利用时间 tn 时的数值,若用单步的欧拉方法,可得到时间tn+1 =  ;tn + h 时的近似值如下:
欧拉方法是一种显型方法,也就是说yn + 1 的解是yi, 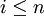 的显函数。
的显函数。
欧拉方法可以求解一阶的微分方程,一个N阶的微分方程可以用导入N − 1 个变数来表示y' , y'', ..., y(N) 的方式,分解为N个一阶的微分方程。因此可以用欧拉方法求解以下的向量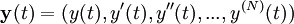 来得到高阶微分方程的解。
来得到高阶微分方程的解。
改进的欧拉算法
先用欧拉法求得一个初步的近似值,称为预报值,然后用它替代梯形法右端的yi+1再直接计算 fi+1,得到校正值yi+1,这样建立的预报-校正系统称为改进的欧拉格式:
预报值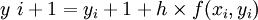
校正值 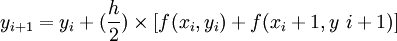
它有下列平均化形式:
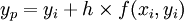
且 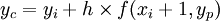
且 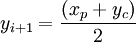
它的局部截断误差为O(h3),可见,改进欧拉格式较欧拉格式提高了精度,其截断误差比欧拉格式提高了一阶。
注:欧拉法用差商 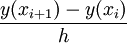 近似代替y(xi)的导数,局部截断误差较大;改进欧拉法先用欧拉法求出预报值,再利用梯形公式求出校正值,局部截断误差比欧拉法低了一阶,较大程度地提高了计算精度。
近似代替y(xi)的导数,局部截断误差较大;改进欧拉法先用欧拉法求出预报值,再利用梯形公式求出校正值,局部截断误差比欧拉法低了一阶,较大程度地提高了计算精度。
Euler-Maruyama discretization("欧拉-丸山"数值解法)的更多相关文章
- HDU2824 The Euler function(欧拉函数)
题目求φ(a)+φ(a+1)+...+φ(b-1)+φ(b). 用欧拉筛选法O(n)计算出n以内的φ值,存个前缀和即可. φ(p)=p-1(p是质数),小于这个质数且与其互质的个数就是p-1: φ(p ...
- hdu2824 The Euler function(欧拉函数个数)
版权声明:本文为博主原创文章,未经博主同意不得转载. vasttian https://blog.csdn.net/u012860063/article/details/36426357 题目链接:h ...
- The Euler function(欧拉函数)
The Euler function Time Limit : 2000/1000ms (Java/Other) Memory Limit : 32768/32768K (Java/Other) ...
- hdu 2824 The Euler function(欧拉函数)
如果打表的话会超内存,我想到了一种方法解决这个问题.题目给出的数据时3000000,我将三百万分成300个数据,将整万的数据存储下来,计算的时候,先计算x和y之间整万的数据,然后再计算零散数据. 想法 ...
- [Project Euler] 来做欧拉项目练习题吧: 题目013
问题描述: Work out the first ten digits of the sum of the following one-hundred 50-digit numbers. 371072 ...
- HDOJ 1787 GCD Again(欧拉函数)
GCD Again Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total ...
- POJ3090_Visible Lattice Points【欧拉函数】
Visible Lattice Points Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 5653 Accepted: 333 ...
- nyoj 1007 GCD(数学题 欧拉函数的应用)
GCD 描述 The greatest common divisor GCD(a,b) of two positive integers a and b,sometimes written (a,b) ...
- 欧拉函数 || LightOJ 1370 Bi-shoe and Phi-shoe
给出x,求最小的y使y的欧拉函数大于等于x *解法:i).求出1e6之内的数的欧拉函数,遍历找 ii).求比x大的第一个质数——因为每个质数n的欧拉函数都是n-1 wa一次是因 ...
随机推荐
- TeamCity : Build 版本控制系统配置
VCS (版本控制系统) 是用来跟踪项目源文件版本变化的系统.它还有其它的名字,比如 SCM(源代码管理).当前 TeamCity 内置支持的 VCS 类型有:Git, Subversion, Mer ...
- 混合框架中Oracle数据库的还原处理操作
在较早期的随笔<Oracle如何实现创建数据库.备份数据库及数据导出导入的一条龙操作>粗略介绍了Oracle数据库的备份还原操作,本文想从开发框架的基础上介绍Oracle数据库的脚本或者还 ...
- java基础练习 字符串,控制流,日历,日期等
1,对基本控制流程的一些练习 package org.base.practice3; import org.junit.Test; /** * Created with IntelliJ IDEA. ...
- 织梦cms常用标签
dedecms简介:织梦内容管理系统(DedeCms) 以简单.实用.开源而闻名,是国内知名的PHP开源网站管理系统,也是使用用户较多的PHP类CMS系统,在经历多年的发展,目前的版本无论在功能,还是 ...
- 两种常用的C语言排序算法
1. 要求输入10个整数,从大到小排序输出 输入:2 0 3 -4 8 9 5 1 7 6 输出:9 8 7 6 5 3 2 1 0 -4 解决方法:选择排序法 实现代码如下: #include &l ...
- spring springMVC
spring是一个开源框架,是为了解决企业应用程序开发,功能如下 目的:解决企业应用开发的复杂性 功能:使用基本的javabean代替EJB,并提供了更多的企业应用功能 范围:任何java应用 总之: ...
- 网址http换成https ----js
<script type="text/javascript"> var url = window.location.href; if (url.indexOf(&quo ...
- js判断网页是否加载完毕 包括图片
<script type="text/javascript" language="JavaScript"> //: 判断网页是否加载完成 docum ...
- jquery手风琴
--js $(document).ready(function(){ //Set default open/close settings$('.acc_container').hide(); //Hi ...
- DataView详解
dataview可以用于对你的datatable筛选,搜索,排序,编辑和导航.可以方便对databale的操作. 先来看一下它有哪些属性: 接下来是方法: 我们怎么使用它呢? public datat ...