PRML读书笔记_绪论曲线拟合部分
一、最小化误差函数拟合
正则化( regularization )技术涉及到给误差函数增加一个惩罚项,使得系数不会达到很大的值。这种惩罚项最简单的形式采用所有系数的平方和的形式。这推导出了误差函数的修改后的形式:
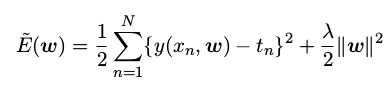
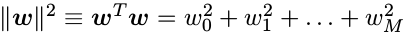
在效果上, λ 控制了模型的复杂性,因此决定了过拟合的程度。
二、贝叶斯曲线拟合
1.正态分布( normal distribution )或者高斯分布( Gaussian distribution )
对于一元实值变量 x ,高斯分布被定义为:
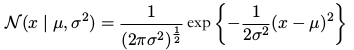
它由两个参数控制:\(μ\) ,被叫做均值( mean ),以及\(σ^2\) ,被叫做方差( variance )。方差的平方根,由 \(σ\) 给定,被叫做标准差( standard deviation )。方差的倒数,记作 \(β = \frac{1}{σ^2}\) ,被叫做精度( precision )。
D 维向量 x 的高斯分布:
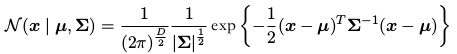
2.曲线拟合
曲线拟合问题的目标是能够根据 N 个输入 \(x = (x_1 , . . . , x_N )^T\) 组成的数据集和它们对应的目标值 \(t = (t_1 , . . . , t_N )^T\) ,在给出输入变量 x 的新值的情况下,对目标变量 t 进行预测。
对应的 t 值服从高斯分布,分布的均值为 y(x, w) ,有:
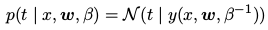
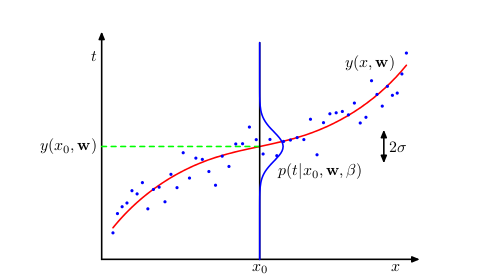
图形化表示:
用训练数据$ {x, t}$ ,通过最大似然方法,来决定未知参数 w 和 β 的值,然函数为:
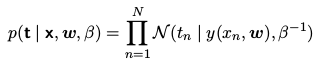
对数似然函数:
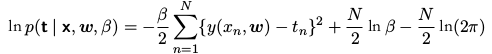
求其最大值就可以求得\(w\)。进一步确定精度参数 \(β\):
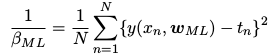
PRML读书笔记_绪论曲线拟合部分的更多相关文章
- PRML读书笔记_绪论
一.基本名词 泛化(generalization) 训练集所训练的模型对新数据的适用程度. 监督学习(supervised learning) 训练数据的样本包含输入向量以及对应的目标向量. 分类( ...
- PRML读书笔记——3 Linear Models for Regression
Linear Basis Function Models 线性模型的一个关键属性是它是参数的一个线性函数,形式如下: w是参数,x可以是原始的数据,也可以是关于原始数据的一个函数值,这个函数就叫bas ...
- 【PRML读书笔记-Chapter1-Introduction】1.2 Probability Theory
一个例子: 两个盒子: 一个红色:2个苹果,6个橘子; 一个蓝色:3个苹果,1个橘子; 如下图: 现在假设随机选取1个盒子,从中.取一个水果,观察它是属于哪一种水果之后,我们把它从原来的盒子中替换掉. ...
- 【PRML读书笔记-Chapter1-Introduction】1.1 Example:Polynomial Curve Fitting
书中给出了一个典型的曲线拟合的例子,给定一定量的x以及对应的t值,要你判断新的x对应的t值多少. 任务就是要我们去发现潜在的曲线方程:sin(2πx) 这时就需要概率论的帮忙,对于这种不确定给t赋何值 ...
- PRML读书笔记——机器学习导论
什么是模式识别(Pattern Recognition)? 按照Bishop的定义,模式识别就是用机器学习的算法从数据中挖掘出有用的pattern. 人们很早就开始学习如何从大量的数据中发现隐藏在背后 ...
- 『TensorFlow』读书笔记_进阶卷积神经网络_分类cifar10_上
完整项目见:Github 完整项目中最终使用了ResNet进行分类,而卷积版本较本篇中结构为了提升训练效果也略有改动 本节主要介绍进阶的卷积神经网络设计相关,数据读入以及增强在下一节再与介绍 网络相关 ...
- 『TensorFlow』读书笔记_进阶卷积神经网络_分类cifar10_下
数据读取部分实现 文中采用了tensorflow的从文件直接读取数据的方式,逻辑流程如下, 实现如下, # Author : Hellcat # Time : 2017/12/9 import os ...
- PRML读书笔记——线性回归模型(上)
本章开始学习第一个有监督学习模型--线性回归模型."线性"在这里的含义仅限定了模型必须是参数的线性函数.而正如我们接下来要看到的,线性回归模型可以是输入变量\(x\)的非线性函数. ...
- The Way to Go读书笔记_第4章_基本结构和基本数据类型
“_”标识符 _ 本身就是一个特殊的标识符,被称为空白标识符.它可以像其他标识符那样用于变量的声明或赋值(任何类型都可以赋值给它),但任何赋给这个标识符的值都将被抛弃,因此这些值不能在后续的代码中使用 ...
随机推荐
- Qt 编程指南 3_1 按钮弹窗手动和自动关联示例
触发的两种模式 connect() 和 on_控件ID_控件函数(参数) 两者优缺点对比: 虽然 Qt 有比较好用的自动关联大法,但自动关联不是万能的,尤其是涉及到多个窗体的时候,比如 A 窗体私有按 ...
- leetcode 199. Binary Tree Right Side View 、leetcode 116. Populating Next Right Pointers in Each Node 、117. Populating Next Right Pointers in Each Node II
leetcode 199. Binary Tree Right Side View 这个题实际上就是把每一行最右侧的树打印出来,所以实际上还是一个层次遍历. 依旧利用之前层次遍历的代码,每次大的循环存 ...
- Spring配置跨域请求
本文主要是Spring+SpringMVC+MyBatis/MyBatis Plus框架环境,包括SpringBoot同样适用. 1.编写拦截器 package com.interceptor; im ...
- MATLAB——神经网络sim仿真函数
- ES6-课程介绍
ES6 可以提高开发效率,把ES3比做斧头,ES5比做锯子,那么ES6就是电锯. ES6新特性 默认参数.字符串模板.结构赋值.箭头函数.set\mat .异步操作.类和对象 .模块化
- DataWorks使用小结(一)——概述
一.概述 DataWorks数据工场,是MaxComputer的可视化开发平台,一站式开发.管理界面 1.功能概述 1.强大调度:支持分钟到月的调度 2.多种任务:支持ODPS.SHELL等多种任务 ...
- 面试2——java基础2
11.MVC设计模型 mvc设计模型是一种使用model-view-controller(模型-视图-控制器)设计创建web应用程序的模式.是一种开发模式,好处是可以将界面和业务逻辑分离. model ...
- ES6入门之let、cont
一.前提 解决ES5中只有全局作用域和函数作用域,没有块级作用域而带来的不合理的场景. let 基本用法 用法和var 一样,只是let声明的变量只有在let命令所在的代码块有效 { let a = ...
- Docker(五):Docker 三剑客之 Docker Machine
上篇文章Docker(四):Docker 三剑客之 Docker Compose介绍了 Docker Compose,这篇文章我们来了解 Docker Machine . Docker Machine ...
- 并行编程(Parallel Framework)
前言 并行编程:通过编码方式利用多核或多处理器称为并行编程,多线程概念的一个子集. 并行处理:把正在执行的大量的任务分割成小块,分配给多个同时运行的线程.多线程的一种. 并行编程分为如下几个结构: 1 ...
