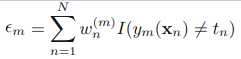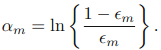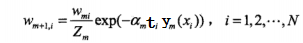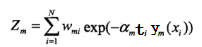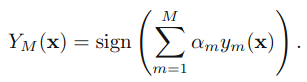AdaBoost--从原理到实现(Code:Python)
本文对原文有修改,若有疑虑,请移步原作者. 原文链接:blog.csdn.net/dark_scope/article/details/14103983
集成方法在函数模型上等价于一个多层神经网络,两种常见的集成方法为Adaboost模型和RandomTrees模型。其中随机森林可被视为前馈神经网络,而Adaboost模型则等价于一个反馈型多层神经网络。
一.引入
对于Adaboost,可以说是久闻大名,据说在Deep Learning出来之前,SVM和Adaboost是效果最好的 两个算法,而Adaboost是提升树(boosting tree),所谓“ 提升树 ” 就是把“弱学习算法”提升(boost)为“强学习算法”(语自《统计学习方法》),而其中最具代表性的也就是Adaboost了,貌似Adaboost的结构还和Neural Network有几分神似,我倒没有深究过,不知道是不是有什么干货。
二.过程
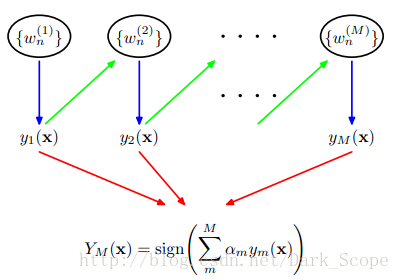
这就是Adaboost的结构,最后的分类器YM是由数个弱分类器(weak classifier)组合而成的,相当于最后m个弱分类器来投票决定分类,而且每个弱分类器的“话语权”α不一样。
这里阐述下算法的具体过程:
1.初始化所有训练样例的权重为1 / N,其中N是样例数
2.for m=1,……M:
a).训练弱分类器ym(),使其最小化权重误差函数(weighted error function):
b)接下来计算该弱分类器的话语权α:
c)更新权重:
其中Zm:
是规范化因子,使所有w的和为1。(这里公式稍微有点乱)
3.得到最后的分类器:
三.原理
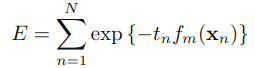
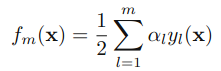
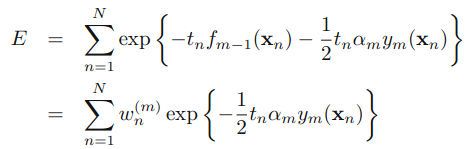
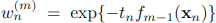 ,可以被看做一个常量,因为它里面没有αm和ym:
,可以被看做一个常量,因为它里面没有αm和ym: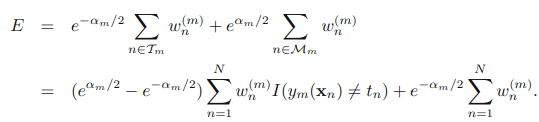
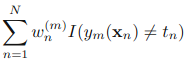
四.实现
# coding: UTF-8
from __future__ import division
import numpy as np
import scipy as sp
from weakclassify import WEAKC
from dml.tool import sign
class ADABC:
def __init__(self,X,y,Weaker=WEAKC):
'''''
Weaker is a class of weak classifier
It should have a train(self.W) method pass the weight parameter to train
pred(test_set) method which return y formed by 1 or -1
see detail in <统计学习方法>
'''
self.X=np.array(X)
self.y=np.array(y)
self.Weaker=Weaker
self.sums=np.zeros(self.y.shape)
self.W=np.ones((self.X.shape[1],1)).flatten(1)/self.X.shape[1]
self.Q=0
#print self.W
def train(self,M=4):
'''''
M is the maximal Weaker classification
'''
self.G={}
self.alpha={}
for i in range(M):
self.G.setdefault(i)
self.alpha.setdefault(i)
for i in range(M):
self.G[i]=self.Weaker(self.X,self.y)
e=self.G[i].train(self.W)
#print self.G[i].t_val,self.G[i].t_b,e
self.alpha[i]=1/2*np.log((1-e)/e)
#print self.alpha[i]
sg=self.G[i].pred(self.X)
Z=self.W*np.exp(-self.alpha[i]*self.y*sg.transpose())
self.W=(Z/Z.sum()).flatten(1)
self.Q=i
#print self.finalclassifer(i),'==========='
if self.finalclassifer(i)==0: print i+1," weak classifier is enough to make the error to 0"
break
def finalclassifer(self,t):
'''''
the 1 to t weak classifer come together
'''
self.sums=self.sums+self.G[t].pred(self.X).flatten(1)*self.alpha[t]
#print self.sums
pre_y=sign(self.sums)
#sums=np.zeros(self.y.shape)
#for i in range(t+1):
# sums=sums+self.G[i].pred(self.X).flatten(1)*self.alpha[i]
# print sums
#pre_y=sign(sums)
t=(pre_y!=self.y).sum()
return t
def pred(self,test_set):
sums=np.zeros(self.y.shape)
for i in range(self.Q+1):
sums=sums+self.G[i].pred(self.X).flatten(1)*self.alpha[i]
#print sums
pre_y=sign(sums)
return pre_y


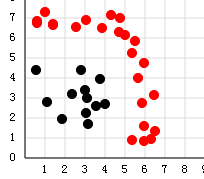
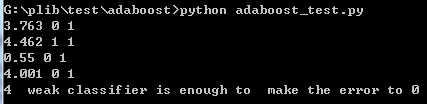
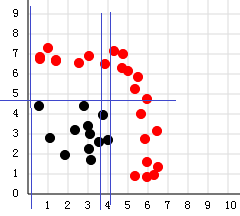
 )
)Reference:
AdaBoost--从原理到实现(Code:Python)的更多相关文章
- 集成学习值Adaboost算法原理和代码小结(转载)
在集成学习原理小结中,我们讲到了集成学习按照个体学习器之间是否存在依赖关系可以分为两类: 第一个是个体学习器之间存在强依赖关系: 另一类是个体学习器之间不存在强依赖关系. 前者的代表算法就是提升(bo ...
- 决策树ID3原理及R语言python代码实现(西瓜书)
决策树ID3原理及R语言python代码实现(西瓜书) 摘要: 决策树是机器学习中一种非常常见的分类与回归方法,可以认为是if-else结构的规则.分类决策树是由节点和有向边组成的树形结构,节点表示特 ...
- paip.日志中文编码原理问题本质解决python
paip.日志中文编码原理问题本质解决python 默认的python日志编码仅仅gbk...保存utf8字符错误..输出到个eric5的控制台十默认好像十unicode的,要是有没显示出来的字符,大 ...
- AdaBoost算法原理简介
AdaBoost算法原理 AdaBoost算法针对不同的训练集训练同一个基本分类器(弱分类器),然后把这些在不同训练集上得到的分类器集合起来,构成一个更强的最终的分类器(强分类器).理论证明,只要每个 ...
- 集成学习之Adaboost算法原理
在boosting系列算法中,Adaboost是最著名的算法之一.Adaboost既可以用作分类,也可以用作回归. 1. boosting算法基本原理 集成学习原理中,boosting系列算法的思想:
- VS Code Python 全新发布!Jupyter Notebook 原生支持终于来了!
VS Code Python 全新发布!Jupyter Notebook 原生支持终于来了! 北京时间 2019 年 10 月 9 日,微软发布了全新的 VS Code Python 插件,带来了众多 ...
- 官宣!VS Code Python 全新功能在 PyCon China 全球首发!
北京时间 2019 年 9 月 21 日,PyCon China 2019 在上海举行. 在下午的演讲中,来自微软开发工具事业部的资深研发工程师 在演讲中,我们看到了 Azure Notebook 与 ...
- MAC+VS Code+Python+Markdown调试配置
目录 VS Code官网下载 VS Code插件推荐 VS Code Python环境配置 Markdown配置 VS Code官方文档 VS Code官网下载 VS Code官网下载地址 VS Co ...
- 基于单层决策树的AdaBoost算法原理+python实现
这里整理一下实验课实现的基于单层决策树的弱分类器的AdaBoost算法. 由于是初学,实验课在找资料的时候看到别人的代码中有太多英文的缩写,不容易看懂,而且还要同时看代码实现的细节.算法的原理什么的, ...
- 集成学习之Adaboost算法原理小结
在集成学习原理小结中,我们讲到了集成学习按照个体学习器之间是否存在依赖关系可以分为两类,第一个是个体学习器之间存在强依赖关系,另一类是个体学习器之间不存在强依赖关系.前者的代表算法就是是boostin ...
随机推荐
- vue 底部bottomnav
<template> <div id="foot"> <div class="tabBar"> <div class= ...
- 【POJ 1860】Currency Exchange
[题目链接]:http://poj.org/problem?id=1860 [题意] 给你n种货币,m种货币之间的交换信息; 交换信息以 A,B,RA,CA,RB,CB的形式给出; 即A换B的话假设A ...
- 剖析Spark-Shell
打开spark-shell,我们可以看到 function main() { if $cygwin; then stty -icanon min 1 -echo > /dev/null 2> ...
- [转] C# 隐藏方法和重写方法
1:方法重写:就是在基类中的方法用virtual关键字来标识,然后在继承类中对该类进行重写 (override),这样基类中的方法在子类中已经被重写了,基类中的方法在子类中已经失去了功能 了.当让基类 ...
- sgu 194 无源汇有上下界的最大流(最大流模板dinic加优化)
模板类型的题具体参考国家集训队论文:http://wenku.baidu.com/view/0f3b691c59eef8c75fbfb35c.html 参考博客:http://blog.csdn.ne ...
- 《高性能MySQL》笔记-BLOB与TEXT
BLOB和TEXT都是为存储很大的数据而设计的字符串数据类型,分别采用二进制和字符方式存储. 实际上,它们分别属于两组不同的数据类型家族: 字符类型是TINYTEXT,SMALLTEXT,TEXT,M ...
- 51nod——1432 独木桥
https://www.51nod.com/onlineJudge/questionCode.html#!problemId=1432 基准时间限制:1 秒 空间限制:131072 KB 分值: 10 ...
- Android studio图片ERROR: 9-patch image xx .9.png malformed
Android studio 图片错误 9-patch image error in Android ERROR: 9-patch image xx .9.png malformed 1) 异常: ...
- MFC 小知识总结四
1 PlaySound 播放WAV格式的音乐 This function plays a sound specified by a file name, resource, or system ev ...
- C语言之文件操作07——读取文件数据并计算均值方差标准差
//文件 /* =============================================================== 题目:从文本文件"high.txt" ...