cf-Round551-Div2-D. Serval and Rooted Tree（DP）

题目链接：https://codeforces.com/contest/1153/problem/D

题意：有一棵树，给定结点数n，在每个结点上的操作（max：表示该结点的number为其孩子结点中的最大值，min相反），结点2..n的父结点。叶子结点上定义的操作可忽略，叶子结点的number为1..num，且互不相同，num为叶子结点个数，求根节点的number的最大值。

思路：被这道题虐了大半天，加上还没找到详细易懂的题解，所以做了这么久，不过弄懂之后还是觉得很值得哈哈。先用vector数组存储每个结点的子节点，用dp[i]表示结点i的最大number是其所有叶子结点中的第dp[i]大的，并且dp[j]=1（j为所有叶子结点的编号）。然后对于非叶子结点，若其操作为max，dp[i]=min(dp[j])（j为i的直接孩子结点，因为求最大值，故是第x大中的x越小越好）;若操作为min，则dp[i]=sum(dp[j])（j为i的直接孩子结点），最终答案为num+1-dp[1]（num为叶子结点个数）。举个例子：

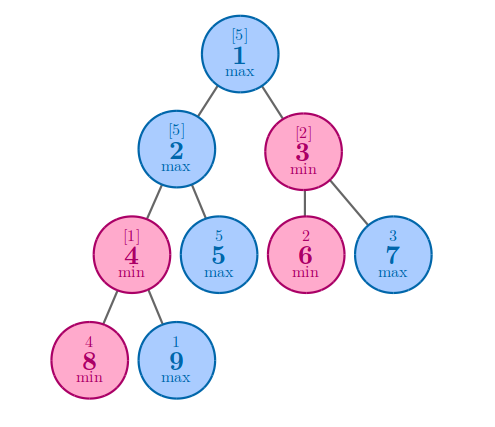
图中的方括号内的数字是其number大小。则dp[4]=dp[8]+dp[9]=2，其实际意义是很明显的，结点4是结点8和结点9中最小的，也就是结点4是其所有叶子孩子结点（结点8、9）中第二大的。dp[2]=min(dp[4],dp[5])=dp[5]=1，也就是结点2是其所有叶子孩子结点（结点5、8、9）中第1大的。dp[3]=sum(dp[6],dp[7])=2，也就是结点3是其所有直接叶子结点（结点6，7）中第二大的。dp[1]=min(dp[2],dp[3])=dp[2]=1，也就是结点1是其所有叶子结点（结点5、6、7、8、9）中第一大的。记num为所有叶子结点的个数，本题num=5，则最终答案为num+1-dp[1]=5-1+1=5。

AC代码：

#include<bits/stdc++.h>
using namespace std;

inline int read(){
    int x=,f=;char c=;
    while(!isdigit(c)){f|=c=='-';c=getchar();}
    while(isdigit(c)){x=(x<<)+(x<<)+(c^);c=getchar();}
    return f?-x:x;
}

const int maxn=;
int n,op[maxn],dp[maxn],num;
vector<int> v[maxn];

void dfs(int p){
    if(p>&&v[p].empty()){
        dp[p]=,++num;
        return;
    }
    if(op[p]) dp[p]=0x3f3f3f3f;
    else dp[p]=;
    for(int i=;i<v[p].size();++i){
        dfs(v[p][i]);
        if(op[p]) dp[p]=min(dp[p],dp[v[p][i]]);
        else dp[p]+=dp[v[p][i]];
    }
}

int main(){
    n=read();
    for(int i=;i<=n;++i)
        op[i]=read();
    for(int i=;i<=n;++i){
        int tmp=read();
        v[tmp].push_back(i);
    }
    dfs();
    printf("%d\n",num+-dp[]);
    return ;
}