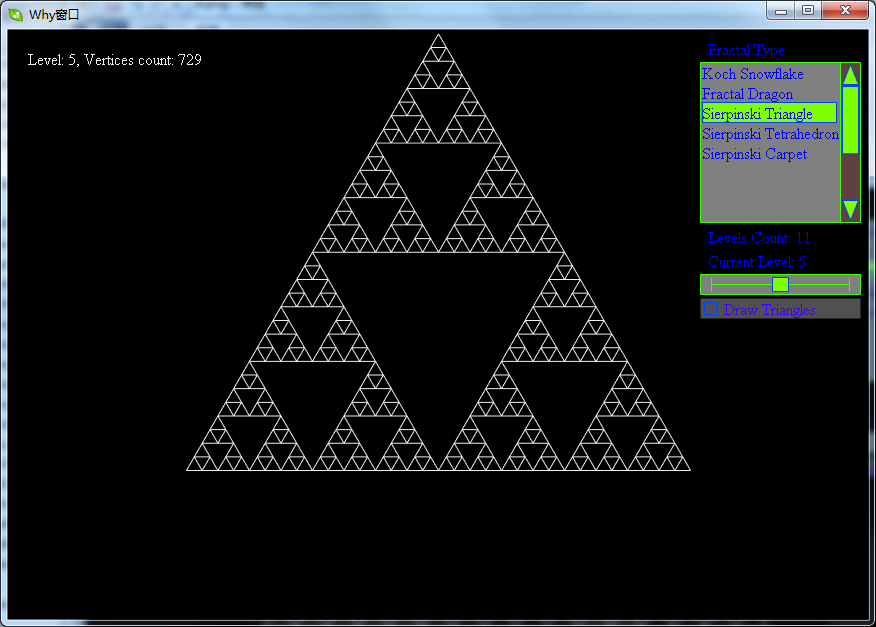
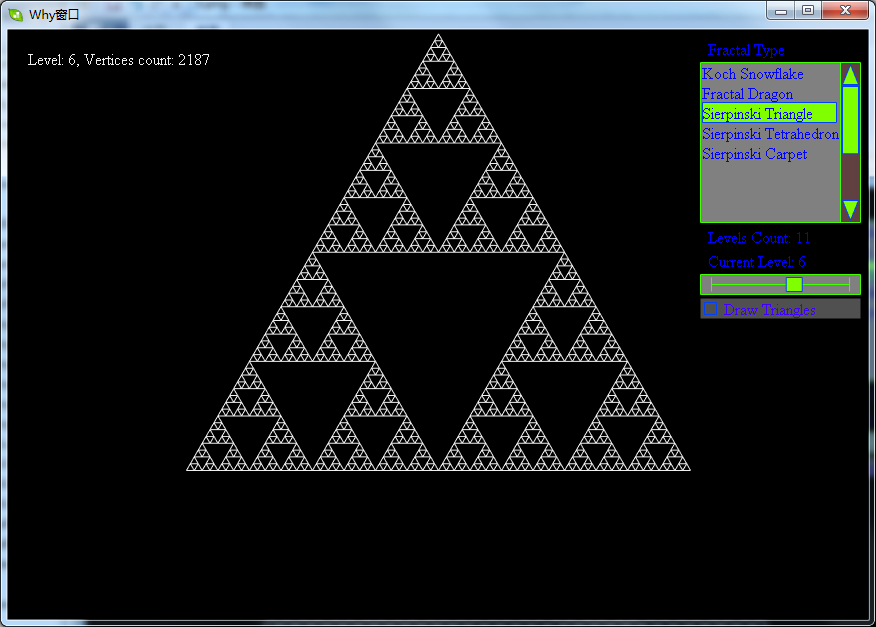
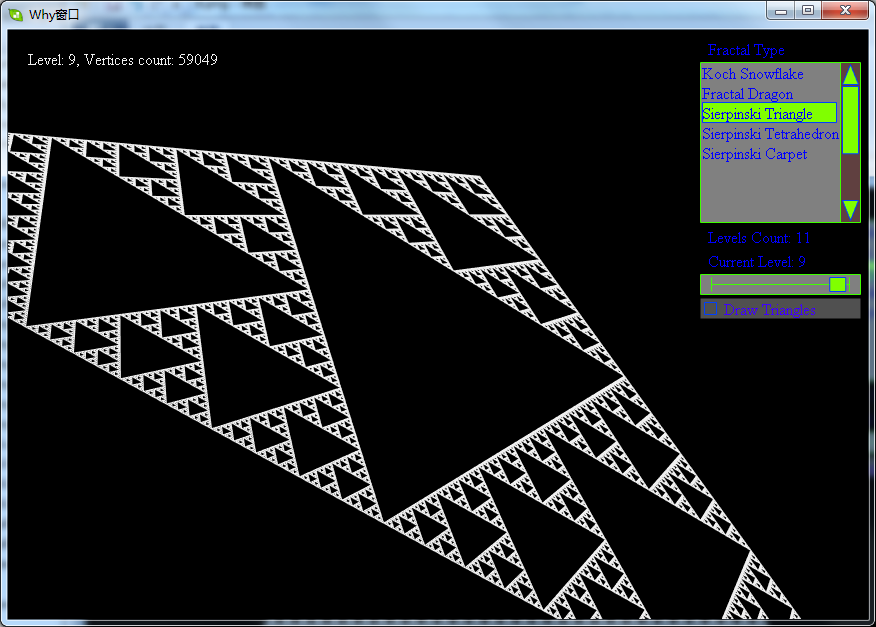
分形之谢尔宾斯基(Sierpinski)三角形

谢尔宾斯基三角形（英语：Sierpinski triangle）是一种分形，由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集。也有的资料将其称之为谢尔宾斯基坟垛.

其生成过程为:

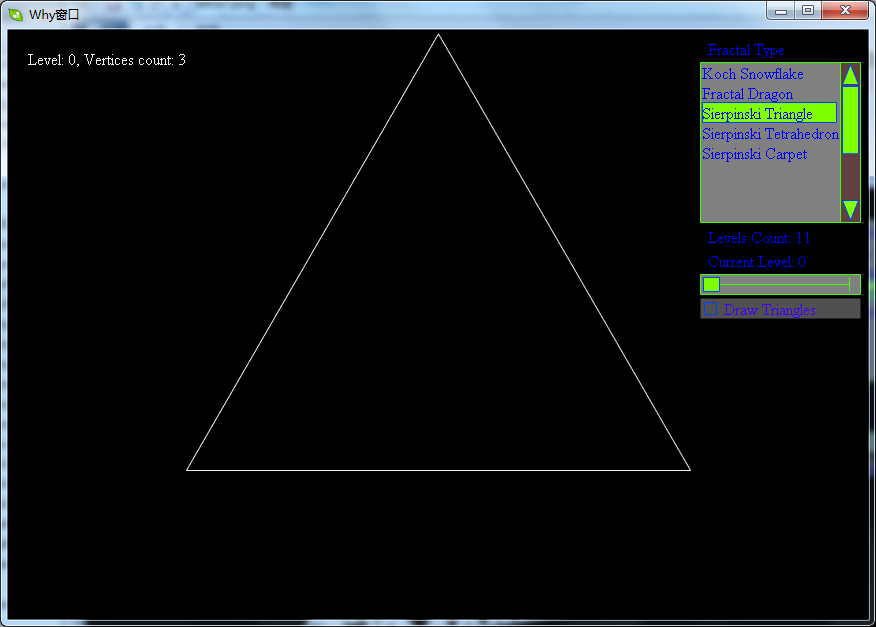
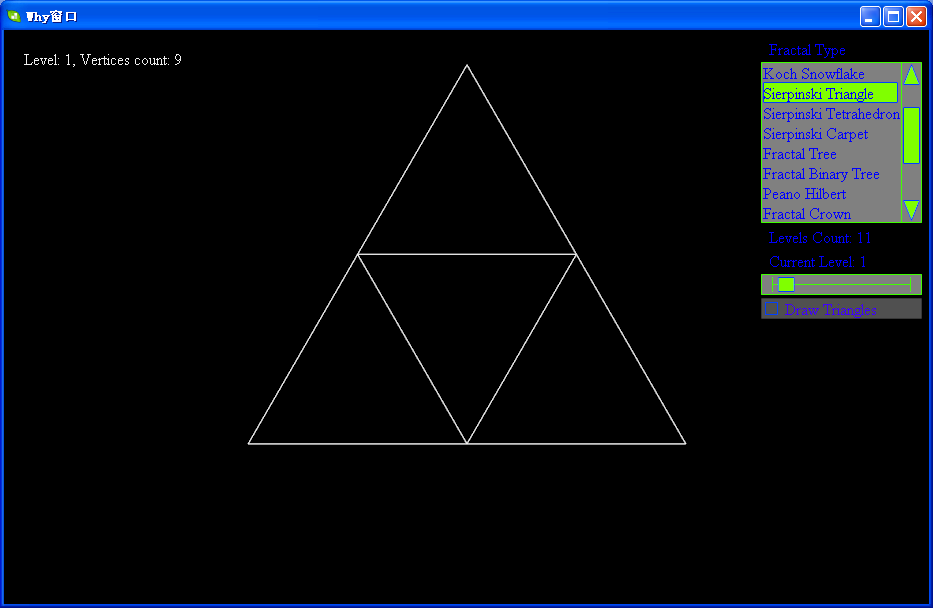
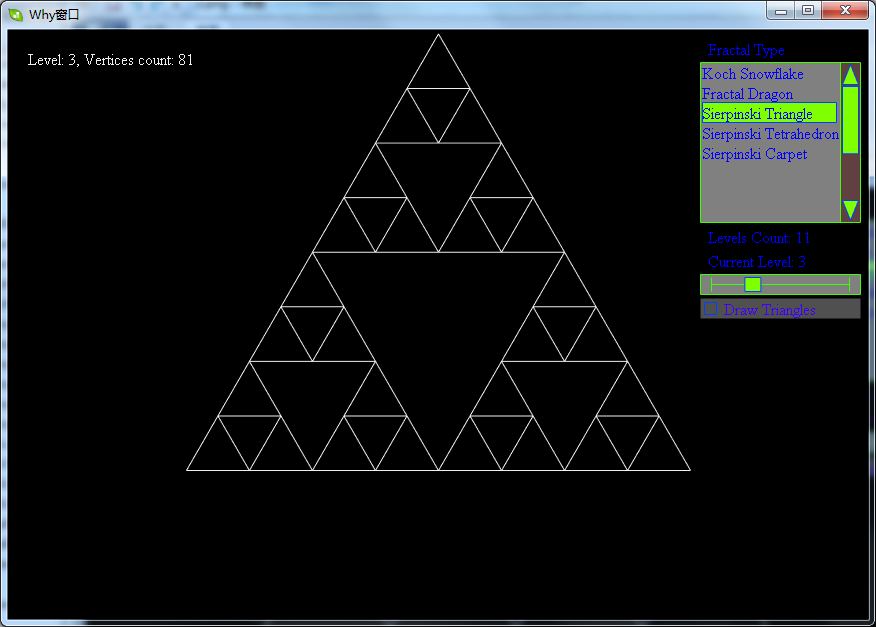
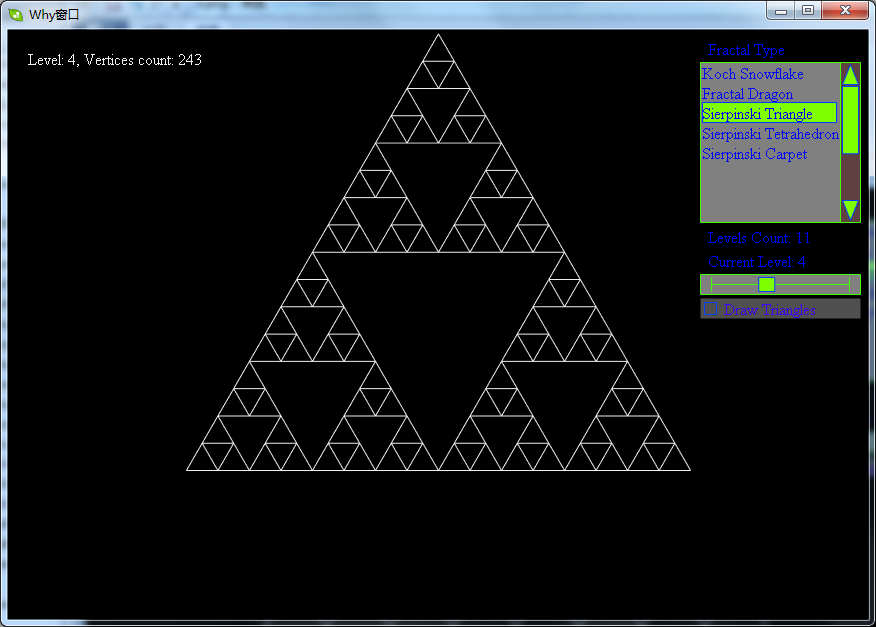
1. 取一个实心的三角形。（多数使用等边三角形）
2. 沿三边中点的连线，将它分成四个小三角形。
3. 去掉中间的那一个小三角形。
4. 对其余三个小三角形重复1。

核心代码:

static void SierpinskiTriangle(const Vector3& v1, const Vector3& v2, const Vector3& v3, Vector3* pVertices)
{
    Vector3 v12 = (v1 + v2)*0.5f;
    Vector3 v13 = (v1 + v3)*0.5f;
    Vector3 v23 = (v2 + v3)*0.5f;

    pVertices[] = v1;
    pVertices[] = v12;
    pVertices[] = v13;

    pVertices[] = v2;
    pVertices[] = v23;
    pVertices[] = v12;

    pVertices[] = v3;
    pVertices[] = v13;
    pVertices[] = v23;
}

软件下载地址:http://files.cnblogs.com/WhyEngine/Fractal.7z