bzoj千题计划203：bzoj3994: [SDOI2015]约数个数和

http://www.lydsy.com/JudgeOnline/problem.php?id=3994

设d(x)为x的约数个数，给定N、M，求

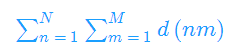
用到的一个结论：

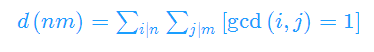
证明：

枚举n的约数i，枚举m的约数j

那么i*j一定是n*m的约数

d（nm）相当于不同的i*j 的个数

若i， j 不互质

设gcd（i，j）= g ， 则 i= p*g ，j=q*g

那么i*j 可以 组成两个互质数p*g*g 和 q 的乘积

p*g*g 和 q 也都输n和m的约数

即p*g*g 和 q 也都是合法的i，j

所以 互质数i和j的乘积组成了n*m的所有的约数

上式得证

回到这个题

令N<=M

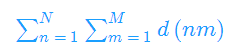
化为

改变枚举顺序，先枚举i，j

当n=[1,N]中所有i的倍数时，i会取n/i次

即i会取 次    （ 里面有除号的[]表示下取整，下面一样）

j 同理

所以 上式化为

=  

=

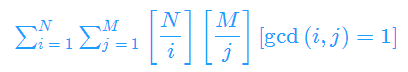
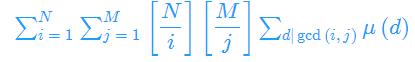
改变枚举顺序，先枚举d

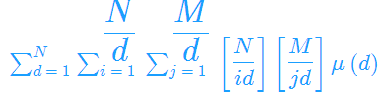
令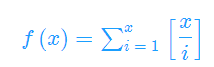 

则

ans=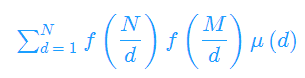

f（x） 可以 用除法分块 提前 N*sqrt(N)处理好

预处理 μ 的前缀和

最后的式子 也可以用除法分块 在sqrt(N)时间内计算出

#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

#define N 50001

typedef long long LL;

int prime[N];
bool vis[N];
int miu[N],sum[N];

LL f[N];

void read(int &x)
{
    x=; char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) { x=x*+c-''; c=getchar(); }
}

void premiu()
{
    int cnt=;
    miu[]=;
    for(int i=;i<N;++i)
    {
        if(!vis[i])
        {
            prime[++cnt]=i;
            miu[i]=-;
        }
        for(int j=;j<=cnt;++j)
        {
            if(prime[j]*i>=N) break;
            vis[i*prime[j]]=true;
            if(i%prime[j]==) break;
            miu[i*prime[j]]=-miu[i];
        }
    }
    for(int i=;i<N;++i) sum[i]+=sum[i-]+miu[i];
}

LL pref(int x)
{
    LL tot=;
    int j;
    for(int i=;i<=x;i=j+)
    {
        j=x/(x/i);
        tot+=(LL)(j-i+)*(x/i);
    }
    return tot;
}

int main()
{
    premiu();
    for(int i=;i<N;++i) f[i]=pref(i);
    int T,n,m,j;
    LL ans;
    read(T);
    while(T--)
    {
        ans=;
        read(n); read(m);
        if(n>m) swap(n,m);
        for(int i=;i<=n;i=j+)
        {
            j=min(n/(n/i),m/(m/i));
            ans+=f[n/i]*f[m/i]*(sum[j]-sum[i-]);
        }
        cout<<ans<<'\n';
    }
}