Locality Sensitive Hashing，LSH

1. 基本思想

局部敏感（Locality Senstitive）：即空间中距离较近的点映射后发生冲突的概率高，空间中距离较远的点映射后发生冲突的概率低。

局部敏感哈希的基本思想类似于一种空间域转换思想，LSH算法基于一个假设，如果两个文本在原有的数据空间是相似的，那么分别经过哈希函数转换以后的它们也具有很高的相似度；相反，如果它们本身是不相似的，那么经过转换后它们应仍不具有相似性。

假设一个局部敏感哈希函数具有10个不同的输出值，而现在我们具有11个完全没有相似度的数据，那么它们经过这个哈希函数必然至少存在两个不相似的数据变为了相似数据。从这个假设中，我们应该意识到局部敏感哈希是相对的，而且我们所说的保持数据的相似度不是说保持100%的相似度，而是保持最大可能的相似度。

对于局部敏感哈希保持最大可能的相似度的这一点，我们也可以从数据降维的角度去考虑。数据对应的维度越高，信息量也就越大，相反，如果数据进行了降维，那么毫无疑问数据所反映的信息必然会有损失。哈希函数从本质上来看就是一直在扮演数据降维的角色。

2. Min-Hashing

定义：特征矩阵按行进行一个随机的置换后，第一个列值为1的行的行号。

对于两个数据\(C_1\)和\(C_2\)，在Min-Hashing方法中，hash值相等的概率等于这两个数据降维前的Jaccard相似度（两个集合的交比两个集合的并）。用公式描述即：
\[
Pr[h_\pi(C_1) = h_\pi (C_2)] = sim(C_1, C_2)
\]

每一个置换等同于一个hash函数，多个置换构成一个hash函数族。假设我们拥有n个hash函数，要求在原始空间相似的两个数据在hash之后得到的n个值均相等的条件过于苛刻，所得到的精确率是很高，但是同样的召回率也会非常低。因此，我们放松了要求，在n个hash函数划分为b个hash函数族，只要两个数据在某一个hash函数族的值均相等，就认为这两个数据相似。

在上述定义下，两个数据在低维空间相似的概率为：\(1−(1−s^r)^b\)。解释如下：

对于两个数据的任意一个函数族来说，这两个函数族值相同的概率是：\(s^r\)，其中s∈[0,1]是这两个文档的相似度。
也就是说，这两个函数族不相同的概率是\(1−s^r\)
这两个文档一共存在b个函数族，这bb个函数族都不相同的概率是\((1−s^r)^b\)
所以说，这b个函数族至少有一个相同的概率是\(1-(1−s^r)^b\)

以上过程可以为一个简单的AND-OR逻辑，这个逻辑同样也应用于下述基于p稳定分布的LSH中。

3. E2LSH：p稳定分布

定义：对于一个实数集R上的分布D，如果存在P>=0，对任何n个实数v1,…,vn和n个满足D分布的变量X1,…,Xn，随机变量\(\sum_iv_ix_i\)和\((\sum_i|v_i|^{p})^{1/p}x\)有相同的分布，其中\(x\)是服从D分布的一个随机变量，则称D为一个p稳定分布。

利用p稳定分布可以有效的近似高维特征向量，并在保证度量距离的同时，对高维特征向量进行降维，其关键思想是，产生一个d维的随机向量\(X\)，随机向量\(X\)中的每一维随机、独立得从p稳定分布中产生。对于一个d维的特征向量\(V\)，如定义，随机变量\(X.V\)具有和\((\sum_i|v_i|^{p})^{1/p}X\)一样的分布，因此可以用\(X.V\)表示向量\(V\)来估算\(||V||_p\) 。

p-稳定 LSH通过涉入p稳定分布和点积的概念，实现了LSH算法在欧几里得空间下的直接应用，而不需要嵌入Hamming空间。p-stable LSH中，度量是欧几里得空间下的lp准则，即向量v1与v2的距离定义为||v1-v2||p，然后通过设定的哈希函数将原始点映射到直线的等长线段上，每条线段便相当于一个哈希桶，与LSH方法类似，距离较近的点映射到同一哈希桶（线段）中的概率大，距离较远的点映射到同一哈希桶中的概率小，正好符合局部敏感的定义。

hash函数：p稳定分布下的hash函数为\(h_{x, b} (v) = \left \lfloor \frac{x.v + b}{w} \right \rfloor\)，用于将d维的特征向量映射到整数集。其中\(x\)为d维向量，每一维都独立取自于p稳定分布，b为[0，w]范围内的随机数。其作用效果图如下：

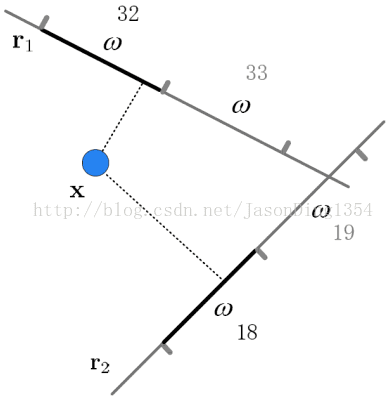
哈希表的设计：将哈希过后的向量直接存入hash表，占用内存又不便于查找。因此论文定义了额外两个hash函数：
\[
h_1(x_1, x_2, ..., x_k) = ((\sum_{i=1}^{k} r_i a_i) mod C) mod tableSize
\]

\[
h_2(x_1, x_2, ..., x_k) = ((\sum_{i=1}^{k} r_i a_i) mod C)
\]

其中，h1的值作为哈希表索引，h2的值作为链表中的关键字，\(r_1\)和\(r_2\)为随机整数，\(C\)的取值为\(2^{32} - 5\)。

4. 缺点

LSH：

典型的基于概率模型生成索引编码的结果并不稳定。虽然编码位数增加，但是查询准确率的提高确十分缓慢；
需要大量的存储空间，不适合于大规模数据的索引。

E2LSH：

E2LSH方法的目标是保证查询结果的准确率和查全率，并不关注索引结构需要的存储空间的大小；
E2LSH使用多个索引空间以及多次哈希表查询，生成的索引文件的大小是原始数据大小的数十倍甚至数百倍。

5. 疑问

\(\sum_iv_ix_i\)和\((\sum_i|v_i|^{p})^{1/p}X\)在满足相同分布的前提下，有什么特点？或则说如果\(X\)不符合p稳定分布，对结果有什么影响？

向量距离的度量可以用范数表示，假设向量\(V = V_1 - V_2\)，那么\(||V||_p\)即表示向量\(V_1\)和\(V_2\)的原始空间下的p范数距离；
点乘的几何意义表示一个向量在另一个向量下的投影表示，因此\(V_1.X - V_2.X = X.V = \sum_iv_ix_i\)表示的是向量\(V_1\)和\(V_2\)在向量\(X\)下投影的距离；
在\(X\)满足p稳定分布的前提下，可知（1）和（2）下的两个距离具有相同的分布，即满足了局部敏感的特点。

6. 参考