BP神经网络的公式推导

如果感觉自己看不懂，那就看看我博客的梯度下降法，博文最后的感知机也算最简单的BP神经网络吧，用的也是反馈(w,b)：典型梯度下降法

BP网络的结构

BP网络的结构如下图所示，分为输入层(Input)，隐含层（Hidden），输出层(Output)。 
输入层的结点个数取决于输入的特征个数。 
输出层的结点个数由分类的种类决定。 
在输入层和输出层之间通常还有若干个隐含层，至于隐含层的个数以及每个隐含层的结点个数由训练工程师的经验来人为设定。 
链接A曾提到由万能逼近定理，一般一个隐含层就足够了。且这个隐含层一般结点个数为： 
 。 
其中：I为输入层结点个数，O为输出层结点个数，a为1～10范围内的调节常数。

就车牌识别中识别数字0～9的BP网络来说：输入层的每个结点就是的待训练的图像每种特征，常见的车牌数字识别有从上到下的每个结点缩放成规定大小的0~9数字图像的每个像素点值。那么输出的结点就只有0～9十个结点。

输入层与隐含层的权重矩阵记为：W_IK，其中隐含层的每个结点与输入层的每个结点都相连，输入层的每个结点与隐含层之间都有一个权重，这样W_IK就是一个I*H的矩阵，同理W_HO就是一个H*O的矩阵。

为了便于后续公式的推导以及明确各个参数的意义，这里特地说明，如下图： 
输入层的结点个数为I， 
隐含层的结点个数为H， 
输出层的结点个数为O；

设输入层有任一结点i， 
设隐含层有任一结点k， 
设输出层有任一结点j；

其中结点i与结点k之间的权重为W_ik开始训练前由人为设定初始值; 
其中结点k与结点j之间的权重为W_kj开始训练前由人为设定初始值;

对于输出层 
设结点j的教师信号为S_j，注：教师信号就是实际值（训练值） 
j的当前偏置为B_j开始训练前由人为设定初始值, 
设结点j的初始输出的结果为y_j， 
设结点j的最终输出结果为Y_j,
注意：Y_j是y_j经过激励函数作用后的值->     Y_j = f(y_j)

对于隐含层： 
隐含层没有教师信号， 
设k的当前偏置为B_k开始训练前由人为设定初始值; 
设结点k的初始输出的结果为y_k, 
设结点k的最终输出结果为Y_k, 
注意：Y_k是y_k经过激励函数作用后的值->   Y_k=f(y_k)

对于输入层： 
输入层结点没有教师信号，没计算值，没有阈值，只有一个结点值 
结点i的值为X_i,

BP算法思想

激励函数

下面解释为什么每个结点要由一开始的输出结果经过激励函数处理下： 
因为y_i其实是由Y_i与B_j以及W_ij以线性函数的形式得到，而根据整个BP算法设计思想要根据每次结点的输出来偏微分来调整每个结点的权重来实现训练目的(这也就是所谓的梯度下降法)，这就需要输出是基于输入的可微分函数，同时为方便归一化的比较输出层每个结点每次输出的结果，就采用下述两种激励函数。

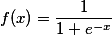
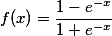
在一般情形下： 

下面对他进行求导，后面解释原理时要用： 

则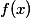的导数为：：

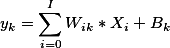　     .................... (X1)   

前向传播

在BP神经网络中，每个节点的输出值是根据上层所有节点的输出值、当前节点与上一层所有节点的权值 和 当前节点的阀值 还有 激活函数来实现的。以上图为例结点k输出值的计算方法：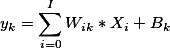 
　.............................(X2)

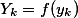        ................ ....................... (X3)

以上图为例结点j输出值的计算方法：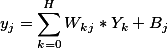 
    ............................(X4)

   .............................................(X5)

其中f为激活函数，就是上面求导的那个函数。

其实，正向传播很简单，就是结点依次执行这两个公式，从输入层到隐含层，从隐含层到输出层。

返向传播

在BP神经网络的输出层，经过网络处理的输入数据的输出结果与标准结果（教师信号）的误差可以用如下的公式来衡量：：

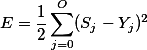    .............................(X6)

网络的返向传播过程就是误差信号的返向传播过程，主要目的就是通过反复修正权值和阀值，使得误差函数值达到最小。而这其中修正权值与阈值的是通过梯度下降法来实现。根据梯度下降法的原理，权值的修正值与误差函数成正比：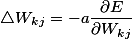 

...............................(X7)

对上述公式进行展开与推导： 
 
令：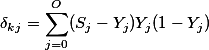

则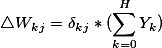：  注：此处少乘以一个α

同样对于B_j有：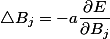 

对上述公式进行展开与推导： 
 
同样令：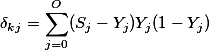

则：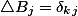　

由上述公式可以得到输出层结点j到隐含层的返向传播的权重W与偏置B的更新策略如下：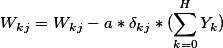 

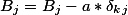
下面推导隐含层到输入层的权重与偏置的梯度： 

令：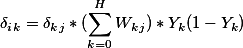

由上述公式可以得到隐含层结点k到输入层的返向传播的权重W与偏置B的更新策略如下：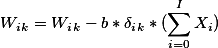 
  注：此处少了一个σ_{kj 隐藏层到输出层的学习因子}

在实际的训练中BP就是不停的迭代实现前向传播与返向传播来修正权重与偏置，得到最终的网络。 
在实际的BP网络测试中，对于一个测试目标提取输入层需要的特征作为输入层结点的值，用上面训练好的网络来进行前向传播，最终输出结点处的值最大的结点，就是这个测试目标的分类。

转载自：http://blog.csdn.net/lanxuecc/article/details/51754838#t0

http://blog.csdn.net/acdreamers/article/details/44657439