MKL库求解矩阵特征值、特征向量(LAPACKE_dgeev、dsyev)
LAPACK(Linear Algebra PACKage)库,是用Fortran语言编写的线性代数计算库,包含线性方程组求解(\(AX=B\))、矩阵分解、矩阵求逆、求矩阵特征值、奇异值等。该库用BLAS库做底层运算。
本示例将重点介绍使用LAPACK库求解非对称矩阵与对称矩阵的特征值、特征向量过程。
1 一般矩阵
在LAPACK库中,使用?geev函数计算一般矩阵的特征值及其左/右特征向量,其中右特征向量\(v_j\)满足
\]
左特征向量\(u_j\)满足
\]
其中\(u_j^H\)表示\(u_j\)的共轭转置。
1.1 参数详解
示例将使用MKL库中,LAPACK中的dgeev函数演示。
lapack_int LAPACKE_dgeev( matrix_order, //(input) 行优先(LAPACK_ROW_MAJOR)或列优先(LAPACK_COL_MAJOR)
jobvl, //(input) 指定是否计算左特征向量,"V":计算;"N":不计算
jobvr, //(input) 指定是否计算右特征向量,同上
n, //(input) 矩阵的阶数
a, //(input/output) 待求解A矩阵
lda, //(input) A矩阵的第一维
wr, //(output) 特征向量实部
wi, //(output) 特征向量虚部
vl, //(output) 左特征向量
ldvl, //(input) 左特征向量第一维
vr, //(output) 右特征向量
ldvr //(input) 右特征向量第一维
)
1.2 定义待求解矩阵
#include <stdlib.h>
#include <stdio.h>
#include "mkl_lapacke.h"
// 参数
#define N 5
#define LDA N
#define LDVL N
#define LDVR N
MKL_INT n = N, lda = LDA, ldvl = LDVL, ldvr = LDVR, info;
double wr[N], wi[N], vl[LDVL*N], vr[LDVR*N];
double a[LDA*N] = {
-1.01, 0.86, -4.60, 3.31, -4.81,
3.98, 0.53, -7.04, 5.29, 3.55,
3.30, 8.26, -3.89, 8.20, -1.51,
4.43, 4.96, -7.66, -7.33, 6.18,
7.31, -6.43, -6.16, 2.47, 5.58
};
1.3 求解特征值、特征向量
LAPACKE_dgeev( LAPACK_ROW_MAJOR, 'V', 'V', n, a, lda, wr, wi, vl, ldvl, vr, ldvr );
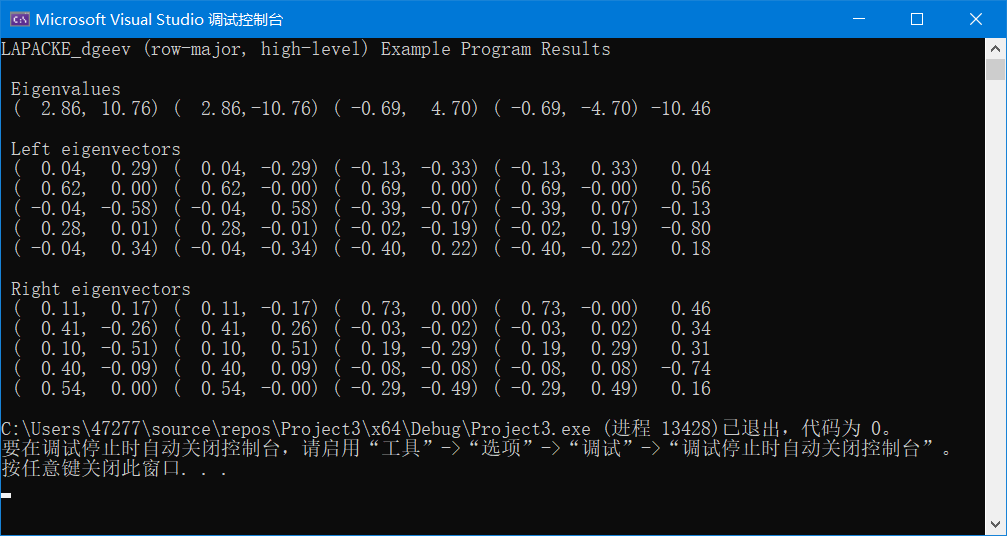
与Matlab中使用eig方法求取特征值与特征向量,所得结果相同。
A = [ -1.01, 0.86, -4.60, 3.31, -4.81;
3.98, 0.53, -7.04, 5.29, 3.55;
3.30, 8.26, -3.89, 8.20, -1.51;
4.43, 4.96, -7.66, -7.33, 6.18;
7.31, -6.43, -6.16, 2.47, 5.58];
[V,D]=eig(A);
Vector = V;
Lambda = diag(D);
display(Lambda);
display(Vector);
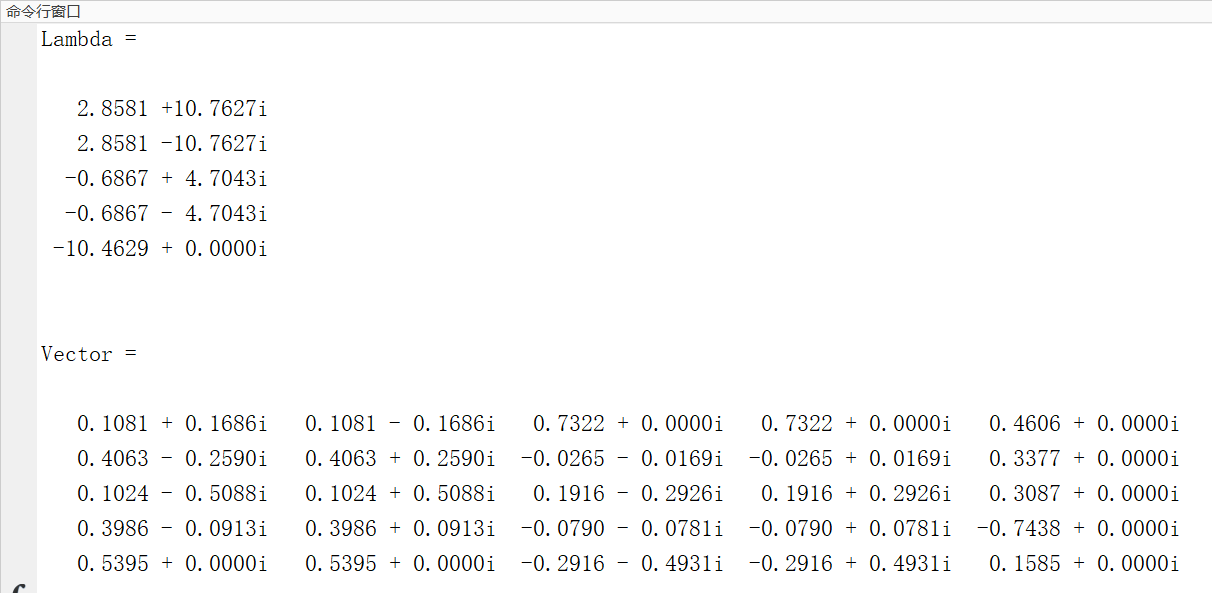
完整代码
#include <stdlib.h>
#include <stdio.h>
#include "mkl_lapacke.h"
//print特征值和特征向量
extern void print_eigenvalues( char* desc, MKL_INT n, double* wr, double* wi );
extern void print_eigenvectors( char* desc, MKL_INT n, double* wi, double* v,
MKL_INT ldv );
#define N 5
#define LDA N
#define LDVL N
#define LDVR N
int main() {
MKL_INT n = N, lda = LDA, ldvl = LDVL, ldvr = LDVR, info;
double wr[N], wi[N], vl[LDVL*N], vr[LDVR*N];
double a[LDA*N] = {
-1.01, 0.86, -4.60, 3.31, -4.81,
3.98, 0.53, -7.04, 5.29, 3.55,
3.30, 8.26, -3.89, 8.20, -1.51,
4.43, 4.96, -7.66, -7.33, 6.18,
7.31, -6.43, -6.16, 2.47, 5.58
};
printf( "LAPACKE_dgeev (row-major, high-level) Example Program Results\n" );
// 求解
info = LAPACKE_dgeev( LAPACK_ROW_MAJOR, 'V', 'V', n, a, lda, wr, wi,
vl, ldvl, vr, ldvr );
if( info > 0 ) {
printf( "The algorithm failed to compute eigenvalues.\n" );
exit( 1 );
}
print_eigenvalues( "Eigenvalues", n, wr, wi );
print_eigenvectors( "Left eigenvectors", n, wi, vl, ldvl );
print_eigenvectors( "Right eigenvectors", n, wi, vr, ldvr );
exit( 0 );
}
void print_eigenvalues( char* desc, MKL_INT n, double* wr, double* wi ) {
MKL_INT j;
printf( "\n %s\n", desc );
for( j = 0; j < n; j++ ) {
if( wi[j] == (double)0.0 ) {
printf( " %6.2f", wr[j] );
} else {
printf( " (%6.2f,%6.2f)", wr[j], wi[j] );
}
}
printf( "\n" );
}
void print_eigenvectors( char* desc, MKL_INT n, double* wi, double* v, MKL_INT ldv ) {
MKL_INT i, j;
printf( "\n %s\n", desc );
for( i = 0; i < n; i++ ) {
j = 0;
while( j < n ) {
if( wi[j] == (double)0.0 ) {
printf( " %6.2f", v[i*ldv+j] );
j++;
} else {
printf( " (%6.2f,%6.2f)", v[i*ldv+j], v[i*ldv+(j+1)] );
printf( " (%6.2f,%6.2f)", v[i*ldv+j], -v[i*ldv+(j+1)] );
j += 2;
}
}
printf( "\n" );
}
}
2 求解对称阵
2.1 参数详解
采用LAPACKE_dsyev方法实现,参数比LAPACKE_dgeev少,含义相似。
lapack_int LAPACKE_dsyev( matrix_layout,
jobz, //是否计算特征值和特征向量, "V"/"N"
uplo, //表示使用A矩阵的上三角或下三角矩阵 "U"/"L"
n,
a,
lda,
w //包含降序的特征值
)
完整代码
#include <stdlib.h>
#include <stdio.h>
#include "mkl_lapacke.h"
extern void print_matrix(const char* desc, MKL_INT m, MKL_INT n, double* a, MKL_INT lda);
#define N 5
#define LDA N
int main() {
MKL_INT n = N, lda = LDA, info;
double w[N];
double a[LDA * N] = {
1.96, - 6.49, - 0.47, - 7.20, - 0.65,
-6.49, 3.80, - 6.39, 1.50, - 6.34,
-0.47, - 6.39, 4.17, - 1.51, 2.67,
-7.20, 1.50, - 1.51, 5.70, 1.80,
-0.65, - 6.34, 2.67, 1.80, - 7.10,
};
printf("LAPACKE_dsyev (row-major, high-level) Example Program Results\n");
//求解特征值、特征向量
info = LAPACKE_dsyev(LAPACK_ROW_MAJOR, 'V', 'U', n, a, lda, w); //'U'表示下三角
if (info > 0) {
printf("The algorithm failed to compute eigenvalues.\n");
exit(1);
}
print_matrix("Eigenvalues", 1, n, w, 1);
print_matrix("Eigenvectors (stored columnwise)", n, n, a, lda);
exit(0);
}
void print_matrix(const char* desc, MKL_INT m, MKL_INT n, double* a, MKL_INT lda) {
MKL_INT i, j;
printf("\n %s\n", desc);
for (i = 0; i < m; i++) {
for (j = 0; j < n; j++) printf(" %6.2f", a[i * lda + j]);
printf("\n");
}
}
输出为:
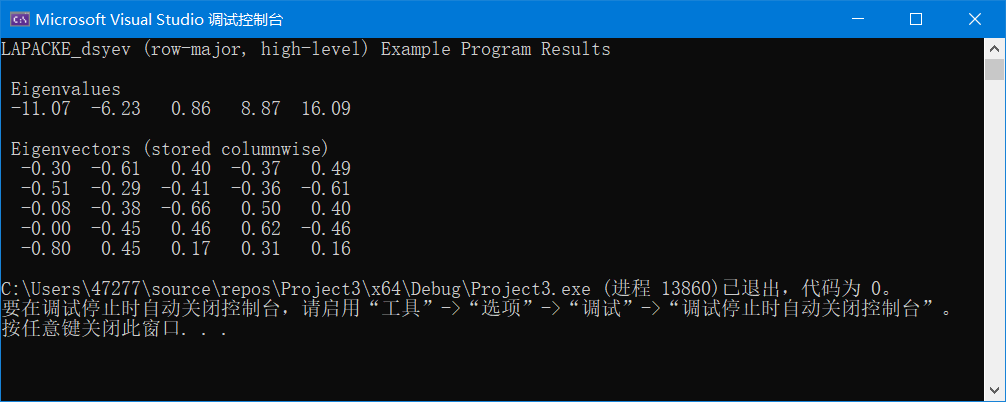
MKL库求解矩阵特征值、特征向量(LAPACKE_dgeev、dsyev)的更多相关文章
- 采用梯度下降优化器(Gradient Descent optimizer)结合禁忌搜索(Tabu Search)求解矩阵的全部特征值和特征向量
[前言] 对于矩阵(Matrix)的特征值(Eigens)求解,采用数值分析(Number Analysis)的方法有一些,我熟知的是针对实对称矩阵(Real Symmetric Matrix)的特征 ...
- MKL库矩阵乘法
此示例是利用Intel 的MKL库函数计算矩阵的乘法,目标为:\(C=\alpha*A*B+\beta*C\),由函数cblas_dgemm实现: 其中\(A\)为\(m\times k\)维矩阵,\ ...
- 使用MTL库求解最小二乘解
最小二乘计算最优解不管是哪个行业肯定都用到的非常多.对于遥感图像处理中,尤其是对图像进行校正处理,关于控制点的几种校正模型中,都用到最小二乘来计算模型的系数.比如几何多项式,或者通过GCP求解RPC系 ...
- MKL库奇异值分解(LAPACKE_dgesvd)
对任意一个\(m\times n\)的实矩阵,总可以按照SVD算法对其进行分解.即: \[A = U\Sigma V^T \] 其中\(U.V\)分别为\(m\times m.n\times n\)的 ...
- [转]Numpy使用MKL库提升计算性能
from:http://unifius.wordpress.com.cn/archives/5 系统:Gentoo Linux (64bit, Kernel 3.7.1)配置:Intel(R) Cor ...
- 如何在 code blocks中使用 mkl库
为了安装caffe, 所以安装了mkl, 现在想在codeblock的项目中使用mkl. 设置mkl环境变量: mkl安装好后默认是在/opt/intel/mkl中,其中/opt/intel/mkl/ ...
- c语言计算矩阵特征值和特征向量-1(幂法)
#include <stdio.h> #include <math.h> #include <stdlib.h> #define M 3 //方阵的行数 列数 #d ...
- 讲一下numpy的矩阵特征值分解与奇异值分解
1.特征值分解 主要还是调包: from numpy.linalg import eig 特征值分解: A = P*B*PT 当然也可以写成 A = QT*B*Q 其中B为对角元为A的特征值的对 ...
- PCA算法是怎么跟协方差矩阵/特征值/特征向量勾搭起来的?
PCA, Principle Component Analysis, 主成份分析, 是使用最广泛的降维算法. ...... (关于PCA的算法步骤和应用场景随便一搜就能找到了, 所以这里就不说了. ) ...
- 特征值 特征向量 正交分解 PCA
无意间想到的,有时间会补充内容. 还记得学线性代数时计算矩阵的特征值和特征向量,然后这个矩阵就可以用这个特征值和特征向量表示. 这样就可以理解成矩阵其实是多个向量拼在一起的,这样就可以将矩阵和向量建立 ...
随机推荐
- 如何查看 linux 发行版本
以 debian 10 buster 为例 有时候我们需要知道当前正在使用的 linux 的发行版本信息...可以通过下面几种方式来查看 使用 lsb_release 命令查看 lsb_release ...
- unity 多层叠加的BillBoard特效转序列帧特效降低overdraw
- MySQL建立RFM模型
1.数据来源 charge_record表数据 提取代码如下: # coding=utf-8import pymysql# 原数据库链接db1 = pymysql.connect( host='*** ...
- Rubymine搭建Ruby开发环境
1.下载和安装Ruby 下载链接:https://rubyinstaller.org/downloads/ 安装示意图: 注意勾选图示的两个选项 安装完成后在cmd窗口运行:ruby -v命令显示当前 ...
- DPDI(Dispatch PDI)kettle调度管理平台基础版安装部署说明
DispatchPDI下载 DPDI online部署包下载地址: Windows: http://files.pizzalord.site/api/public/dl/7Tnq6ScE/releas ...
- kettle介绍-参数变量
ETL中为什么使用参数变量 实现ETL的复用 D,Q,P环境不同,使用变量方便发布 有的条件需要外部传入 增量ETL 灵活性强 kettle中参数变量种类 Environment Variables ...
- CTF靶场学习-XXE漏洞篇
XXE漏洞1(无限制) XXE特征:在HTTP的Request报文出现一下请求报文,即表明此时是采用XML进行数据传输,就可以测试是否存在XML漏洞. 默认xxe,没有任何限制,可以直接读取flag ...
- wpf,前端动画demo,鱼眼效果
如题,鱼眼.特此备注下 1 <Window x:Class="WpfApp2.Window3" 2 xmlns="http://schemas.microsoft. ...
- Spring 中@Autowired,@Resource,@Inject 注解实现原理
使用案例 前置条件: 现在有一个 Vehicle 接口,它有两个实现类 Bus 和 Car ,现在还有一个类 VehicleService 需要注入一个 Vehicle 类型的 Bean: publi ...
- 17.8K star!完美超越宝塔的产品,像呼吸一样部署应用,这款开源神器绝了!
嗨,大家好,我是小华同学,关注我们获得"最新.最全.最优质"开源项目和高效工作学习方法 Dokploy是一个强大的开源平台,旨在简化全栈 Web 应用的开发和部署.通过其直观的界面 ...
