HDU 3516 Tree Construction (四边形不等式)

题意：给定一些点(xi,yi)(xj,yj)满足:i<j,xi<xj,yi>yj。用下面的连起来，使得所有边的长度最小？

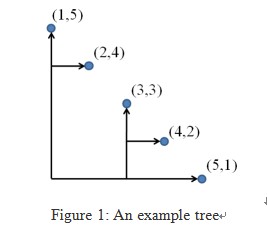
思路:考虑用区间表示，f[i][j]表示将i到j的点连起来的最小代价。

那么f[i][j]=min(f[i][k]+f[k+1][j]+cost(i,j)

cost(i,j)=a[k].y-a[j].y+a[k+1].x-a[i].x;

看起来和四边形不等式有关系，我们需要证明以下(a<b<c<d)

cost(a,c)+cost(b,d)<=cost(a,d)+cost(b,c)

cost(b,c)<=cost(a,d)

有个结论:w为凸当且仅当:cost(i,j)+cost(i+1,j+1)<=cost(i+1,j)+cost(i,j+1)

这个证明只需要固定i,j中的某一个，然后移动另一个即可.

 #include<algorithm>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #include<iostream>
 int f[][],s[][],n;
 struct Point{
     int x,y;
 }a[];
 int cost(int i,int j,int k){
     if (k>=j) return 0x3f3f3f3f;
     return a[k].y-a[j].y+a[k+].x-a[i].x;
 }
 int main(){
     while (~scanf("%d",&n)){
         for (int i=;i<=n;i++){
             scanf("%d%d",&a[i].x,&a[i].y);
         }
         for (int i=;i<=n;i++) s[i][i]=i;
         memset(f,,sizeof f);
         for (int L=;L<=n;L++)
          for (int i=;i+L-<=n;i++){
                 int j=L+i-;f[i][j]=0x3f3f3f3f;
                 for (int k=s[i][j-];k<=s[i+][j];k++){
                     int tmp=f[i][k]+f[k+][j]+cost(i,j,k);
                     if (tmp<f[i][j]) f[i][j]=tmp,s[i][j]=k;
                 }
         }
         printf("%d\n",f[][n]);
     }
 }