Codeforces Codeforces Round #484 (Div. 2) E. Billiard

Codeforces Codeforces Round #484 (Div. 2) E. Billiard

题目连接：

http://codeforces.com/contest/982/problem/E

Description

Consider a billiard table of rectangular size $n \times m$ with four pockets. Let's introduce a coordinate system with the origin at the lower left corner (see the picture).

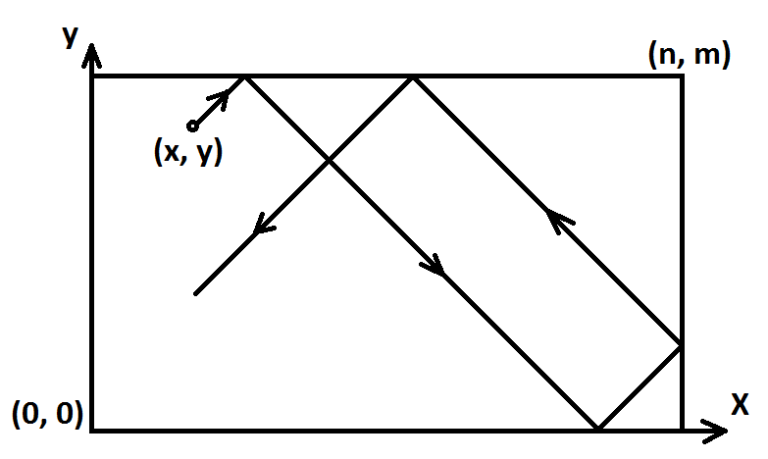
There is one ball at the point $(x, y)$ currently. Max comes to the table and strikes the ball. The ball starts moving along a line that is parallel to one of the axes or that makes a $45^{\circ}$ angle with them. We will assume that:

1. the angles between the directions of the ball before and after a collision with a side are equal,
2. the ball moves indefinitely long, it only stops when it falls into a pocket,
3. the ball can be considered as a point, it falls into a pocket if and only if its coordinates coincide with one of the pockets,
4. initially the ball is not in a pocket.

Note that the ball can move along some side, in this case the ball will just fall into the pocket at the end of the side.

Your task is to determine whether the ball will fall into a pocket eventually, and if yes, which of the four pockets it will be.

Sample Input

4 3 2 2 -1 1

Sample Output

0 0

题意

给定一个球和方向，问能不能在盒子里停下来

Giving a ball and vector, judge it will stop in the box or not

官方题解以及机器翻译。。：

如果您在平面上相对于其两侧对称地反射矩形，则球的新轨迹将更容易。线性轨迹如果是正确的。一个可能的解决方案是

• 如果矢量与轴成90度角，则写入if-s。
• 否则，转动场以使影响矢量变为（1,1）。
• 写出球的直线运动方程： - 1·x + 1·y + C = 0。如果我们用球的初始位置代替，我们可以找到系数C.
• 请注意，在平面的无限平铺中，可以以（k1·n，k2·m）的形式表示任何孔的坐标。
• 用球的线的方程中的点的坐标代替。丢番图方程a·k1 + B·k2 = Cis。如果C |可以解决GCD（A，B）。否则，没有解决方案。
• 在这个丢番图方程的所有解中，我们对正半轴上的最小值感兴趣。
• 通过查找k1，k2可以很容易地得到相应口袋的坐标
• 如果需要，将场转回。

If you symmetrically reflect a rectangle on the plane relative to its sides, the new trajectory of the ball will be much easier. Linear trajectory if be correct. One possible solution is:

• If the vector is directed at an angle of 90 degrees to the axes, then write the if-s.
• Otherwise, turn the field so that the impact vector becomes (1, 1).
• Write the equation of the direct motion of the ball:  – 1·x + 1·y + C = 0. If we substitute the initial position of the ball, we find the coefficient C.
• Note that in the infinite tiling of the plane the coordinates of any holes representable in the form (k1·n, k2·m).
• Substitute the coordinates of the points in the equation of the line of the ball. The Diophantine equation a·k1 + B·k2 = Cis obtained. It is solvable if C | gcd(A, B). Otherwise, there are no solutions.
• Of all the solutions of this Diophantine equation, we are interested in the smallest on the positive half-axis.
• By finding k1, k2 it is easy to get the coordinates of the corresponding pocket
• Rotate the field back if required.

代码

#include <bits/stdc++.h>

using namespace std;

long long x, y, xx, yy;
long long vx, vy;
long long fx, fy;
long long c;

long long ex_gcd(long long a, long long b, long long &xa, long long &ya) {
    if (!b) {
        xa = c;
        ya = 0;
        return a;
    }
    long long ret = ex_gcd(b, a % b, xa, ya);
    long long temp = xa;
    xa = ya;
    ya = temp - (a / b) * ya;
    return ret;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    cerr.tie(nullptr);

    cin >> x >> y >> xx >> yy >> vx >> vy;
    if (!vx) {
        if (xx == 0 || xx == x) {
            if (vy == 1) {
                cout << xx << " " << y;
            } else {
                cout << xx << " " << 0;
            }
        } else
            return 0 * puts("-1");
        return 0;
    }
    if (!vy) {
        if (yy == 0 || yy == y) {
            if (vx == 1) {
                cout << x << " " << yy;
            } else {
                cout << 0 << " " << yy;
            }
        } else
            return 0 * puts("-1");
        return 0;
    }

    if (vx == -1) fx = 1, xx = x - xx;
    if (vy == -1) fy = 1, yy = y - yy;

    c = xx - yy;
    if (c % __gcd(x, y))
        return 0 * puts("-1");
    c /= __gcd(x, y);
    long long m = y / __gcd(x, y);
    long long xxx, yyy;
    ex_gcd(x, y, xxx, yyy);
    xxx = (xxx % m + m - 1) % m + 1;
    yyy = -(yy - xx + x * xxx) / y;
    long long ansn = x, ansm = y;
    if (xxx % 2 == 0) ansn = x - ansn;
    if (yyy % 2 == 0) ansm = y - ansm;
    if (fx) ansn = x - ansn;
    if (fy) ansm = y - ansm;
    cout << ansn << " " << ansm;
}