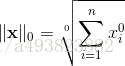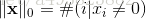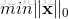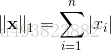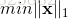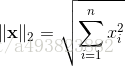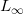范数(norm) 几种范数的简单介绍
原文地址:https://blog.csdn.net/a493823882/article/details/80569888
我们知道距离的定义是一个宽泛的概念,只要满足非负、自反、三角不等式就可以称之为距离。范数是一种强化了的距离概念,它在定义上比距离多了一条数乘的运算法则。有时候为了便于理解,我们可以把范数当作距离来理解。
在数学上,范数包括向量范数和矩阵范数,向量范数表征向量空间中向量的大小,矩阵范数表征矩阵引起变化的大小。一种非严密的解释就是,对应向量范数,向量空间中的向量都是有大小的,这个大小如何度量,就是用范数来度量的,不同的范数都可以来度量这个大小,就好比米和尺都可以来度量远近一样;对于矩阵范数,学过线性代数,我们知道,通过运算AX=B,可以将向量X变化为B,矩阵范数就是来度量这个变化大小的。
这里简单地介绍以下几种向量范数的定义和含义
1、 L-P范数
与闵可夫斯基距离的定义一样,L-P范数不是一个范数,而是一组范数,其定义如下:
根据P 的变化,范数也有着不同的变化,一个经典的有关P范数的变化图如下: 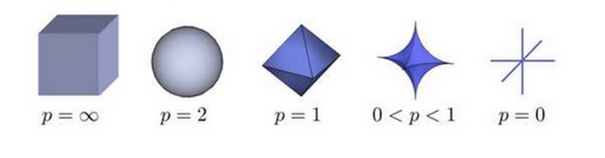
上图表示了p从无穷到0变化时,三维空间中到原点的距离(范数)为1的点构成的图形的变化情况。以常见的L-2范数(p=2)为例,此时的范数也即欧氏距离,空间中到原点的欧氏距离为1的点构成了一个球面。
实际上,在0时,Lp并不满足三角不等式的性质,也就不是严格意义下的范数。以p=0.5,二维坐标(1,4)、(4,1)、(1,9)为例,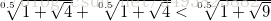
2、L0范数
当P=0时,也就是L0范数,由上面可知,L0范数并不是一个真正的范数,它主要被用来度量向量中非零元素的个数。用上面的L-P定义可以得到的L-0的定义为:
这里就有点问题了,我们知道非零元素的零次方为1,但零的零次方,非零数开零次方都是什么鬼,很不好说明L0的意义,所以在通常情况下,大家都用的是:
对于L0范数,其优化问题为:
s.t. Ax=b 在实际应用中,由于L0范数本身不容易有一个好的数学表示形式,给出上面问题的形式化表示是一个很难的问题,故被人认为是一个NP难问题。所以在实际情况中,L0的最优问题会被放宽到L1或L2下的最优化。
3、L1范数
L1范数是我们经常见到的一种范数,它的定义如下:
L1范数有很多的名字,例如我们熟悉的曼哈顿距离、最小绝对误差等。使用L1范数可以度量两个向量间的差异,如绝对误差和(Sum of Absolute Difference):
对于L1范数,它的优化问题如下:
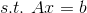
4、L2范数
L2范数是我们最常见最常用的范数了,我们用的最多的度量距离欧氏距离就是一种L2范数,它的定义如下:
表示向量元素的平方和再开平方。
像L1范数一样,L2也可以度量两个向量间的差异,如平方差和(Sum of Squared Difference):

对于L2范数,它的优化问题如下:
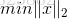
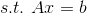
5、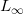
当
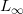
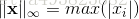
来表示
范数(norm) 几种范数的简单介绍的更多相关文章
- iOS性能检测之Instrunments - 几种常用工具简单介绍
Instrunments: 没错,就是这货,很多人平时开发可能不一定会用到这个,但我要说的是,学会使用它,会让你加分不少哦 先来一张全家福: 1.打开方式 或者 两种方式都行. 2.今天主要介绍一下 ...
- java设计模式三种工厂模式简单介绍
一.简单工厂模式 概述:简单工厂模式的创建意图就是,把对类的创建初始化全都交给一个工厂来执行,而用户不需要去关心创建的过程是什么样的,只用告诉工厂我想要什么就行了.而这种方法的缺点也很明显,违背了设计 ...
- Redis的五种数据类型的简单介绍和使用
1.准备工作: 1.1在Linux下安装Redis https://www.cnblogs.com/dddyyy/p/9763098.html 1.2启动Redis 先把root/redis的red ...
- SpringMVC七种参数绑定简单介绍
a. 默认支持的类型: httpServletRequest, httpservletresponse, httpsession, model 看自己需要, 如果需要用就加 ...
- android:Activity四种启动模式简单介绍
Activity启动模式 能够依据实际的需求为Activity设置相应的启动模式,从而能够避免创建大量反复的Activity等问题 Activity有四种载入模式 1.standard(默认启动模式, ...
- JVM之几种垃圾收集器简单介绍
本文中的垃圾收集器研究背景为:HotSpot+JDK1.7 一.垃圾收集器概述 如上图所示,垃圾回收算法一共有7个,3个属于年轻代.三个属于年老代,G1属于横跨年轻代和年老代的算法. JVM会从年轻代 ...
- (转)几种范数的解释 l0-Norm, l1-Norm, l2-Norm, … , l-infinity Norm
几种范数的解释 l0-Norm, l1-Norm, l2-Norm, - , l-infinity Norm from Rorasa's blog l0-Norm, l1-Norm, l2-Norm, ...
- 简单介绍一下R中的几种统计分布及常用模型
统计学上分布有很多,在R中基本都有描述.因能力有限,我们就挑选几个常用的.比较重要的简单介绍一下每种分布的定义,公式,以及在R中的展示. 统计分布每一种分布有四个函数:d――density(密度函数) ...
- [QT]简单介绍一下 *.pro、*.pri、*.prf、*.prl等四种文件
转自:http://blog.csdn.net/dbzhang800/article/details/6348432 简单介绍一下 *.pro.*.pri.*.prf.*.prl等四种文件:干嘛用的, ...
随机推荐
- JAVA-Enum 枚举
[参考]枚举类名建议带上 Enum 后缀,枚举成员名称需要全大写,单词间用下划线隔开. 说明:枚举其实就是特殊的类,域成员均为常量,且构造方法被默认强制是私有. 正例:枚举名字为 ProcessSta ...
- js中得计算问题算式结果拼接成字符串怎么解决
如题:经常遇到类似问题 一种:自定义的弱类型 var savNum=0; var num=$("#numU").val();//jsp页面获得得值 savNum=parseInt( ...
- sqoop 使用
spark 环境搭建 下载解压 wget https://mirrors.tuna.tsinghua.edu.cn/apache/sqoop/1.4.7/sqoop-1.4.7.bin__hadoop ...
- tedu训练营day01
1.三大操作系统 1.Unix :MacOS 2.Linux :Ubuntu18.04 .CentOS.RedHat 3.Windows :Win7.Win8.Win102.VMware Workst ...
- ext Table中CommandColumn用法
<ext:CommandColumn Width="250" Header="功能菜单" ColumnID="test" Butto ...
- 群发技术-使用python3给微信好友群发消息
本文介绍如何给个人微信好友群发消息. 微信个人号中的群发助手可以一次给30个发送消息,如果要给所有所有群发,则需要自己手动发送多次,或者借助程序实现了.本文即是程序实现教程 一.原理 在微信的官方网站 ...
- Docker 更改默认存储目录 - 十一
Cemtos 7 Docker 默认目录是 /var/lib/docker docker info 查看 docker 配置信息 更改 docker 默认目录 : 编辑 启动文件: 编辑 /usr/ ...
- matplotlib的安装和允许中文及几种字体
安装 python -m pip install matplotlib 允许中文: 使用matplotlib的字体管理器指定字体文件 plt.rcParams['font.sans-serif'] ...
- Python的参数类型
参数类型: 1.必填参数,位置参数(positional arguments,官方定义,就是其他语言所说的参数) 2.默认值参数,非必传 3.可变参数,非必传,不限制参数个数,比如说给多个人发邮件,发 ...
- Linux和进程内存模型
一.Linux和进程内存模型 jvm是一个进程的身份运行在linux系统上,了解linux和进程的内存关系,是理解jvm和Linux内存关系的基础. 硬件.系统.进程三个层面的内存之间的概要关系 1. ...