PID控制器开发笔记之四：梯形积分PID控制器的实现

从微积分的基本原理看，积分的实现是在无限细分的情况下进行的矩形加和计算。但是在离散状态下，时间间隔已经足够大，矩形积分在某些时候显得精度要低了一些，于是梯形积分被提出来以提升积分精度。

1、梯形积分基本思路

在PID控制其中，积分项的作用是消除余差，为了尽量减小余差，应提高积分项的运算精度。在积分项中，默认是按矩形方式来计算积分，将矩形积分改为梯形积分可以提高运算精度。其计算公式为：

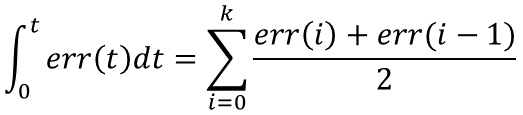
于是如果在位置型PID算法中引入梯形积分则可以修改计算公式如下：

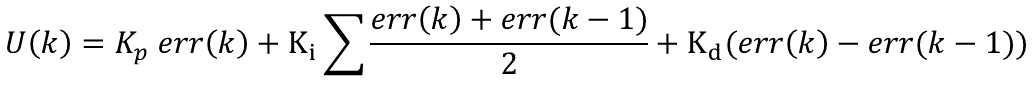
同样要在增量型PID算法中引入梯形积分则可以修改计算公式如下：

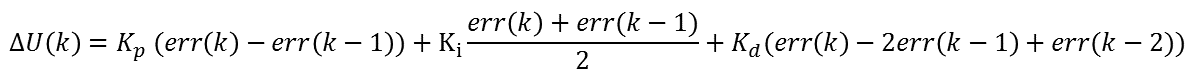
2、算法实现

从微积分的角度来说，当微分分到无限小时，矩形积分与梯形积分是没有区别的。但事实上我们的采样时间不可能无限小，而且也不可能是连续的，那么采样周期越大，那么矩形近似于实际曲线间的偏差就越大，而梯形积分则可以更加接近实际曲线，所以采用梯形积分代替矩形积分就可以得到更高的精度。

（1）位置型PID算法实现

位置型PID的实现在前面就已经完成，所不同的是前面使用的是矩形积分，在这一节我们将举行积分部分改为梯形积分，同样首先定义PID对象的结构体：

 /*定义结构体和公用体*/

 typedef struct

 {

   float setpoint;       //设定值

   float proportiongain;     //比例系数

   float integralgain;      //积分系数

   float derivativegain;    //微分系数

   float lasterror;     //前一拍偏差

   float result; //输出值

   float integral;//积分值

 }PID;

接下来实现PID控制器：

 void PIDRegulation(PID *vPID, float processValue)

 {

   float thisError;

   thisError=vPID->setpoint-processValue;

   vPID->integral+=(thisError+ vPID-> lasterror)/;

   vPID->result=vPID->proportiongain*thisError+vPID->integralgain*vPID->integral+vPID->derivativegain*(thisError-vPID->lasterror);

   vPID->lasterror=thisError;

 }

从上述实现我们不难看出，变化仅仅只是在做积分累计vPID->integral时，将累计量按梯形方式累计。

（2）增量型PID算法实现

同样的增量型PID的梯形积分实现也就是即将积分部分有矩形积分部分换成梯形积分即可。首先定义PID对象的结构体：

 /*定义结构体和公用体*/

 typedef struct

 {

   float setpoint;       //设定值

   float proportiongain;     //比例系数

   float integralgain;      //积分系数

   float derivativegain;    //微分系数

   float lasterror;     //前一拍偏差

   float preerror;     //前两拍偏差

   float deadband;     //死区

   float result; //输出值

 }PID;

接下来实现PID控制器：

 void PIDRegulation(PID *vPID, float processValue)

 {

   float thisError;

   float increment;

   float pError,dError,iError;

   thisError=vPID->setpoint-processValue; //得到偏差值

   pError=thisError-vPID->lasterror;

   iError=(thisError+ vPID-> lasterror)/;

   dError=thisError-*(vPID->lasterror)+vPID->preerror;

   increment=vPID->proportiongain*pError+vPID->integralgain*iError+vPID->derivativegain*dError;   //增量计算

   vPID->preerror=vPID->lasterror;  //存放偏差用于下次运算

   vPID->lasterror=thisError;

   vPID->result+=increment;

 }

3、总结

积分项的引入目的就是为了消除系统的余差，那么积分项的计算精度越高，对消除系统的余差就越有利。梯形积分相较于矩形积分其精度有比较大的提高，所以对消除余差也就越有效。

欢迎关注：