P6772 [NOI2020]美食家

题目大意

给你一个 \(n\) 个点，\(m\) 条边的有向图，每条边有一个权值 \(w_i\) ，每个节点有一个权值 \(a_i\) 。

你从节点 \(1\) 出发，每经过一个节点就可以获得该点的权值 \(a_i\) （起始点也可以获得，每个节点可以重复获得），问你经过的边权和恰好为 \(T\) 时，能获得的最大（点）权值和。

同时，题目还给出 \(k\) 个特殊条件，如果你在到达第 \(x_i\) 个节点时经过的边权和恰好为 \(t_i\) ，那么你就可以额外获得 \(y_i\) 的权值。

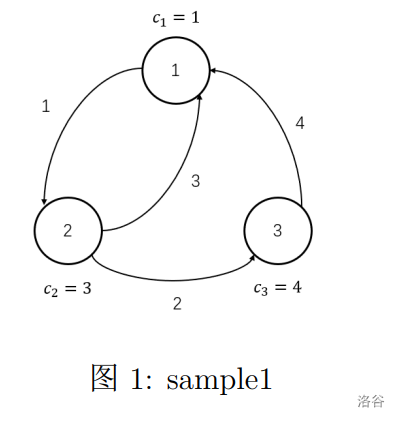
题解

我们可以观察题目数据范围：

对于所有测试点：

\(1≤n≤50\)，\(n \leq m \leq 501\)，\(0 \leq k \leq 200\)，\(1 \leq t_i \leq T \leq 10^9\)。

\(1\leq wi \leq 5\)，\(1 \leq c_i \leq 52501\)，\(1 \leq u_i, v_i, x_i \leq n\)，\(1 \leq y_i \leq 10^9\)。

发现每条边的边权不超过 \(5\) ，又考虑到我们需要恰好经过的边权为 \(T\) ，所以我们可以通过将边拆成点，同时建一个 \(floyd\) 矩阵，我们就可以利用矩阵快速幂来解决这个问题了。

但是我们发现还有一些特殊情况需要处理，我们可以考虑分段，每一段中间用矩阵快速幂，每一个相应的特殊情况给对应的位置添加值。

这样的复杂度是 $ O(125_n^3k~logT)$ ，肯定是不行的，所以我们考虑优化。

由于我们每一次乘上的矩阵都是一样的，所以我们考虑预处理 \(2^k\) 的矩阵幂，然后每一个段都用类似于倍增的方式去处理。

这样的复杂度是 \(O(25~n^2~k~logT+125~n^3~logT)\) ，是可以接受的。

以上。

代码如下：

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=55,M=505,K=205;
int n,m,t,k;
int u,v,w;
int a[N],ksm[35];
struct Matrix
{
	int n,m;
	int h[N*5][N*5];
	Matrix() {n=m=0,memset(h,-1,sizeof(h));}
	void print()
	{
		for(int i=1;i<=n;++i)
		{
			for(int j=1;j<=m;++j)
			printf("%lld ",h[i][j]);
			printf("\n");
		}
		printf("\n");
	}
}res[35],sta;
Matrix operator*(const Matrix a,const Matrix b)
{
	Matrix ans;
	ans.n=a.n,ans.m=b.m;
	for(int i=1;i<=ans.n;++i)
	{
		for(int j=1;j<=ans.m;++j)
		{
			for(int k=1;k<=a.m;++k)
			{
				if(a.h[i][k]>=0&&b.h[k][j]>=0)
				ans.h[i][j]=max(ans.h[i][j],a.h[i][k]+b.h[k][j]);
			}
		}
	}
	return ans;
}
struct Festival {int t,x,y;}s[K];
bool cmp(Festival a,Festival b) {return a.t<b.t;};
signed main()
{
	// freopen("delicacy.in","r",stdin);
	// freopen("delicacy.out","w",stdout);
	cin>>n>>m>>t>>k;
	for(int i=1;i<=n;++i)
	scanf("%lld",&a[i]);
	res[0].n=res[0].m=n*5;
	for(int i=1;i<=n*5;++i)
	{
		if(i/5==(i-1)/5)
		res[0].h[i][i+1]=0;
	}
	for(int i=1;i<=m;++i)
	scanf("%lld%lld%lld",&u,&v,&w),
	res[0].h[(u-1)*5+w][(v-1)*5+1]=a[v];
	for(int i=1;i<=32;++i)
	res[i]=res[i-1]*res[i-1];
	sta.n=1,sta.m=n*5;
	sta.h[1][1]=a[1];
	for(int i=1;i<=k;++i)
	scanf("%lld%lld%lld",&s[i].t,&s[i].x,&s[i].y);
	sort(s+1,s+1+k,cmp);
	ksm[0]=1;
	for(int i=1;i<=32;++i)
	ksm[i]=(ksm[i-1]<<1);
	int tmp=0;
	for(int i=1;i<=k;++i)
	{
		for(int j=32;j>=0;--j)
		{
			if(tmp+ksm[j]<=s[i].t)
			tmp+=ksm[j],sta=sta*res[j];
		}
		if(sta.h[1][(s[i].x-1)*5+1]>=0)
		sta.h[1][(s[i].x-1)*5+1]+=s[i].y;
	}
	for(int i=32;i>=0;--i)
	{
		if(tmp+ksm[i]<=t)
		tmp+=ksm[i],sta=sta*res[i];
	}
	printf("%lld\n",sta.h[1][1]);
	return 0;
}