何时用SVG何时用canvas

SVG

矢量图,视觉清晰,文件小

<svg viewBox="0 0 100 100">
  <circle cx="50" cy="50" r="50" />
  <style>
    circle { fill: blue; animation: pulse 2s alternate infinite; }
    @keyframes pulse {
      100% {
        r: 30;
      }
    }
  </style>
  <script>
    document.querySelector('circle').addEventListener('click', e => {
      e.target.style.fill = "red";
    });
  </script>
</svg>

关键可以放在一起玩

Canvas

是javascript绘图API

大佬提出来的想法是:

SVG是默认选择,画布是备份,简单的说当你不能使用SVG时候才使用canvas

canvas 元素

参考资料

<canvas id="tutorial" width="150" height="150"></canvas>

渲染上下文

var canvas = document.getElementById('tutorial');
var ctx = canvas.getContext('2d');

编写一个基本骨架

 <style>
    #canvas{
      border:1px solid #ccc;
    }
  </style>
  <canvas id="canvas" width="150" height="150"></canvas>

绘制矩形

fillRect(x, y, width, height)

绘制一个填充的矩形

strokeRect(x, y, width, height)

绘制一个矩形的边框

clearRect(x, y, width, height)

清除指定矩形区域，让清除部分完全透明。

案例

  let canvas = document.querySelector('#canvas')
  let ctx = canvas.getContext('2d')
  // 填充
  ctx.fillRect(10,10,80,80)
  // 删除部分
  ctx.clearRect(10,10,20,20)
  // 填充边框的矩形
  ctx.strokeRect(10,10,10,10)

绘制路径

创建路径起始点
画图命令绘制路径
路径闭合
路径生成后,通过描边或填充路径来渲染图形

deginpath()

新建一条路径

closePath()

闭合路径

stroke()

通过线条绘制图形轮廓

fill()

通过填充路径绘制成实心的图形

案例

绘制一个三角形
let ctx = canvas.getContext('2d')
  ctx.beginPath()
  ctx.moveTo(50, 50)// 点
  ctx.lineTo(50, 100)// 直线
  ctx.lineTo(130, 100)//
  ctx.fill()

MoveTo(x,y)

将笔触移动到指定的坐标x以及y上

lineTo(x, y)

绘制一条从当前位置到指定x以及y位置的直线。

 // 描边三角形
  ctx.beginPath()
  ctx.moveTo(50, 50)// 点
  ctx.lineTo(50, 100)// 直线
  ctx.lineTo(130, 100)//
  ctx.closePath()
  ctx.stroke()

lineWidth 行宽

strokeStyle 边框的颜色

ctx.lineWidth=5
ctx.strokeStyle='red'

lineCap 线头

butt 默认
round 半圆形
square 移动到末端

      context.lineCap = 'butt';
	 context.lineCap = 'round';
	 context.lineCap = 'square';

lineJoin 线连接

bevel 斜角
round 圆角
square 默认

ctx.lineJoin = "bevel";
ctx.lineJoin = "round";
默认  "square"

圆弧

arc()

度数转为弧度公式

度数*Math.PI/180

方法

arc(x,y,radius,startAngle,endAngle,direction)

画一个以（x,y)为圆心的以radius为半径的圆弧（圆），从startAngle开始到endAngle结束,direction方向true顺时针,false逆时针,默认顺时针true

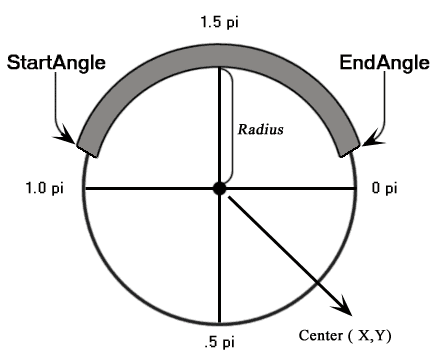
用弧度画一个圆

 let ctx = canvas.getContext('2d')
  ctx.beginPath()
  ctx.moveTo(250, 250)// 点
  ctx.arc(250,250,100,0,2 * Math.PI,)
  ctx.closePath()
  ctx.stroke()

我们要记住开始的弧度和结束的弧度记住上面的公式,一个圆是2*Math.PI

所以半圆是Math.PI

  ctx.arc(250,250,100,1/3*Math.PI,2 * Math.PI,)

开始位置是1/3,结束位置是终点位置

arcTo

arcTo(x1,y1,x2,y2,radius)

画曲线,要想明白它们之间的关系需要画辅助线

 let x0 = 100,
    y0 = 100,
    x1 = 400,
    y1 = 100,
    x2 = 350,
    y2 = 150;
  ctx.beginPath();
  ctx.moveTo(x0, y0);
  ctx.strokeStyle = "#f00";
  ctx.lineWidth = 2;
  ctx.arcTo(x1, y1, x2, y2, 20);
  ctx.stroke();
  ctx.beginPath();
  ctx.strokeStyle = "rgba(0,0,0,0.5)";
  ctx.lineWidth = 1;
  ctx.moveTo(x0, y0);
  ctx.lineTo(x1, y1);
  ctx.fillText('x1,y1', x1 + 10, y1 + 10)
  ctx.lineTo(x2, y2);
  ctx.fillText('x2,y2', x2 + 10, y2)
  ctx.stroke();

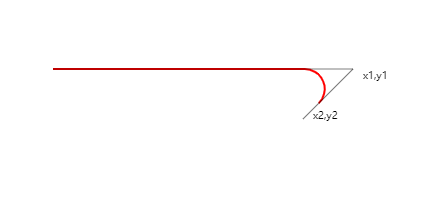
说明一下,x0,y0 起点坐标,x1,y1 第一个点坐标,x2,y2 第二个坐标

arcTo的规律: 他其实是通过起点，第1点，第2点的两条直线，组成了一个夹角，而这两条线，也是参数圆的切线。其中圆的半径决定了圆会在什么位置与线条发生切边。

让我们把球球变大吧！

ctx.arcTo(x1,y1,x2,y2,50); //半径改成50

我们发现他们还是相切的,因为切线可以无限延长

为了方便计算，我先把两条线的夹角改成90度。

var x0=100,

y0=400,

x1 = 500,

y1 = 400,

x2 = 500,

y2 = 450;

更改后就是90度张开了哟！我们保持球的半径不变。刷新后：

我们把y2变大，也就是延长了一条切线，把他变成550，刷新后：

切线是延长了，但arcTo画出的红线没有任何变化。

写一个可行的案例吧

绘制一个背景网格

 // 绘制网格 grid
  for (let x = 0.5; x < 500; x += 10) {
    ctx.moveTo(x, 0);
    ctx.lineTo(x, 500)
  }
  for (let y = 0; y < 500; y += 10) {
    ctx.moveTo(0, y)
    ctx.lineTo(500, y)
  }
  ctx.strokeStyle = '#eee';
  ctx.stroke();

画两条直线相交

  // lines
  ctx.strokeStyle = 'gray';
  ctx.lineWidth = 1;
  ctx.beginPath()
  ctx.moveTo(51, 24)
  ctx.lineTo(314, 540)
  ctx.moveTo(477, 34)
  ctx.lineTo(86, 484)
  ctx.stroke();

绘制两条线上的点

问题来了两点确定一条直线怎么知道线上的点的位置关系

两点式公式

(y-y2)/(y1-y2) = (x-x2)/(x1-x2)

求两条直线上面的交点

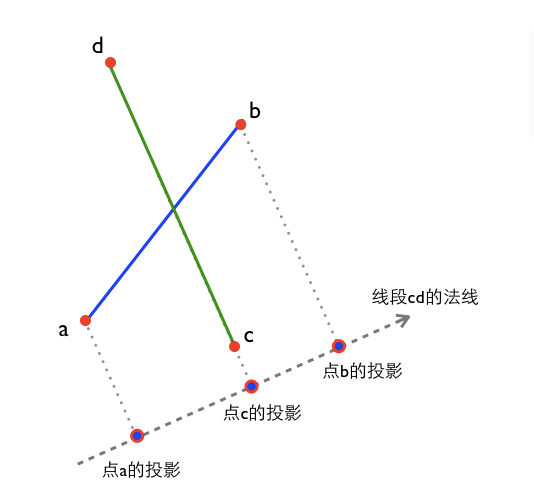
function segmentsIntr(a, b, c, d){
  //线段ab的法线N1
  let nx1 = (b.y - a.y), ny1 = (a.x - b.x);
  //线段cd的法线N2
  let nx2 = (d.y - c.y), ny2 = (c.x - d.x);
  //两条法线做叉乘, 如果结果为0, 说明线段ab和线段cd平行或共线,不相交
  let denominator = nx1*ny2 - ny1*nx2;
  if (denominator==0) {
    return false;
  }
  //在法线N2上的投影
  let distC_N2=nx2 * c.x + ny2 * c.y;
  let distA_N2=nx2 * a.x + ny2 * a.y-distC_N2;
  let distB_N2=nx2 * b.x + ny2 * b.y-distC_N2;
  // 点a投影和点b投影在点c投影同侧 (对点在线段上的情况,本例当作不相交处理);
  if ( distA_N2*distB_N2>=0  ) {
    return false;
  }
  //
  //判断点c点d 和线段ab的关系, 原理同上
  //
  //在法线N1上的投影
  let distA_N1=nx1 * a.x + ny1 * a.y;
  let distC_N1=nx1 * c.x + ny1 * c.y-distA_N1;
  let distD_N1=nx1 * d.x + ny1 * d.y-distA_N1;
  if ( distC_N1*distD_N1>=0  ) {
    return false;
  }
  //计算交点坐标
  let fraction= distA_N2 / denominator;
  let dx= fraction * ny1,
    dy= -fraction * nx1;
  return { x: a.x + dx , y: a.y + dy };
}
console.log(segmentsIntr({x: 51, y: 24}, {x: 314, y: 540}, {x: 477, y: 34}, {x: 86, y: 484}));

上demo代码

  // 两点式公式
  // (y-y2)/(y1-y2) = (x-x2)/(x1-x2)。
  // 我们设y=200,可以求出x=140.7
  ctx.beginPath()
  ctx.moveTo(140.7,200)
  ctx.arc(140.7,200,5,0,2*Math.PI)
  // 设x=350,求右边直线的y点 180.16
  ctx.moveTo(350,180.16)
  ctx.arc(350,180.16,5,0,2*Math.PI)
  // 求原点坐标
  ctx.moveTo(211.713,339.3166)
  ctx.arc(211.713,339.3166,5,0,2*Math.PI)
  ctx.fillStyle = 'red';
  ctx.fill();

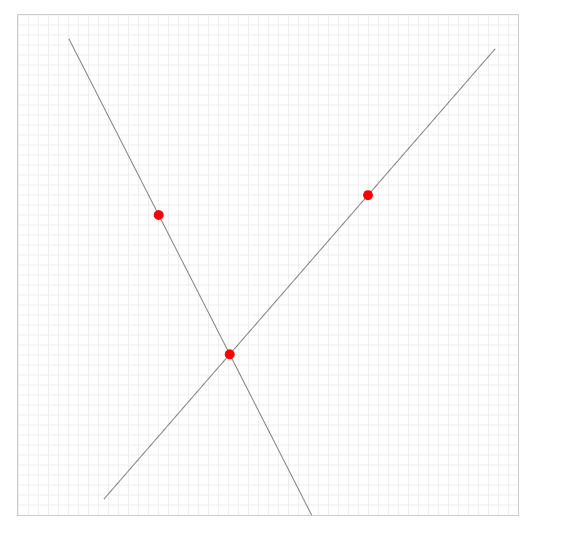
标记点的位置

  ctx.font='14px Arial'
  ctx.beginPath()
  ctx.fillText("(x0,y0)",140.7+5,200+5)
  ctx.fillText("(x1,y1)",350+5,180.16+5)
  ctx.fillText("(x2,y2)",211.713+5,339.3166+5)

画arcTo 曲线

// 编写arcTo
  ctx.beginPath()
  ctx.lineWidth=3;
  ctx.moveTo(140.7,200)
  ctx.arcTo(211.713,339.3166,350,180.16,100)
  ctx.stroke()

问题又来了,我该怎么求这个切点的坐标呢

唉,我这种菜鸡都忘记啦...

我想出来的方法手动移动,我就不写了,都忘光了

全部代码集合

let canvas = document.querySelector('#canvas')
  let ctx = canvas.getContext('2d');
  // 绘制网格 grid
  for (let x = 0.5; x < 500; x += 10) {
    ctx.moveTo(x, 0);
    ctx.lineTo(x, 500)
  }
  for (let y = 0; y < 500; y += 10) {
    ctx.moveTo(0, y)
    ctx.lineTo(500, y)
  }
  ctx.strokeStyle = '#eee';
  ctx.stroke();
  // lines
  ctx.strokeStyle = 'gray';
  ctx.lineWidth = 1;
  ctx.beginPath()
  ctx.moveTo(51, 24)
  ctx.lineTo(314, 540)
  // k=(y2-y1)/(x2-x1)
  ctx.moveTo(477, 34)
  ctx.lineTo(86, 484)
  ctx.stroke();
  // 原点
  // 问题来了两点确定一条直线怎么知道线上的点的位置关系
  // 两点式公式
  // (y-y2)/(y1-y2) = (x-x2)/(x1-x2)。
  // 我们设y=200,可以求出x=140.7
  ctx.beginPath()
  ctx.moveTo(140.7,200)
  ctx.arc(140.7,200,5,0,2*Math.PI)
  // 设x=350,求右边直线的y点 180.16
  ctx.moveTo(350,180.16)
  ctx.arc(350,180.16,5,0,2*Math.PI)
  // 求原点坐标
  ctx.moveTo(211.713,339.3166)
  ctx.arc(211.713,339.3166,5,0,2*Math.PI)
  ctx.fillStyle = 'red';
  ctx.fill();
  // 标记点的坐标
  ctx.font='14px Arial'
  ctx.beginPath()
  ctx.fillText("(x0,y0)",140.7+5,200+5)
  ctx.fillText("(x1,y1)",211.713+5,339.3166+5)
  ctx.fillText("(x2,y2)",350+5,180.16+5)
  // 编写arcTo
  ctx.beginPath()
  ctx.lineWidth=3;
  ctx.moveTo(140.7,200)
  ctx.arcTo(211.713,339.3166,350,180.16,100)
  ctx.stroke()

See the Pen ExyOEBr by 973782523
(@973782523) on CodePen.

这种辅助线有点复杂.那我们可以用简单点的直线辅助线

相信大家已经很熟练了,直接上代码吧

  ctx.strokeStyle = '#eee';
  ctx.stroke();
  // lines
  ctx.strokeStyle = 'gray';
  ctx.lineWidth = 1;
  ctx.beginPath()
  ctx.moveTo(81, 24)
  ctx.lineTo(81, 400)
  ctx.moveTo(400, 300)
  ctx.lineTo(40, 300)
  ctx.stroke();
  // 原点
  ctx.beginPath()
  ctx.moveTo(81, 200)
  ctx.arc(81, 200, 5, 0, 2 * Math.PI)
  ctx.moveTo(220, 300)
  ctx.arc(220, 300, 5, 0, 2 * Math.PI)
  // 求原点坐标
  ctx.moveTo(81, 300)
  ctx.arc(81, 300, 5, 0, 2 * Math.PI)
  ctx.fillStyle = 'red';
  ctx.fill();
  // 标记点的坐标
  ctx.font = '14px Arial'
  ctx.beginPath()
  ctx.fillText("(x0,y0)", 81 + 5, 200 + 5)
  ctx.fillText("(x1,y1)", 81 + 5, 300 + 5)
  ctx.fillText("(x2,y2)", 220 + 5, 300 + 5)
  // 编写arcTo
  ctx.beginPath()
  ctx.lineWidth = 3;
  ctx.moveTo(81, 200)
  ctx.arcTo(81, 300, 220, 300, 100)
  ctx.stroke()

canvas基础[一]探究出初中数学知识的更多相关文章

用初中数学知识撸一个canvas环形进度条
周末好,今天给大家带来一款接地气的环形进度条组件vue-awesome-progress.近日被设计小姐姐要求实现这么一个环形进度条效果,大体由四部分组成,分别是底色圆环,进度弧,环内文字,进度圆点. ...
canvas基础[二]教你编写贝塞尔曲线工具
贝塞尔曲线 bezierCurveTo 在线工具 https://canvature.appspot.com/ [感觉这个好用一些] https://blogs.sitepointstatic.com ...
canvas 基础知识整理（二）
html部分: <canvas id="myCanvas" width="800" height="800" ></can ...
canvas 基础知识
canvas 基础低版本的ie不支持html5,需要引入excanvas.js来让ie支持canvas. 检测支持canvas <canvas id="canvas" wi ...
canvas API ，通俗的canvas基础知识（一）
在没学canvas的时候,觉得canvas是这么的神秘,这么的绚丽,这么的高深,用canvas做出来的效果是如此的炫酷,能做的事情如此的宽广,简直让我心生敬畏之心,时常感叹:我要是得此技能,必定要上天 ...
《DirectX 9.0 3D游戏开发编程基础》必备的数学知识读书笔记
最近在看游戏导航源码,但是看了几天感觉看不懂.里面全是一些几何运算,以及一些关于3d方面的知识.发现自己缺少3d这方面的知识,正好也想研究一下3d游戏开发的基本原理,于是决定买本书看看了,后来在ope ...
canvas绘图数学知识总结
题外话: 最近看了一本书叫 <HTML5 Canvas核心技术图形.动画与游戏开发>已经算是看了85%,基本接近尾声,所以近期会多总结一些关于canvas的东西, 这本书讲的还算可以,最 ...
canvas基础知识
canvas基础知识 ## CanvasDOM对象 #### 获取绘图环境```canvas.getContext();``` #### 设置宽和高```canvas.width = 500;canv ...
canvas 基础知识整理（一）
canvas这个 HTML 元素是为了客户端矢量图形而设计的.它自己没有行为,但却把一个绘图 API 展现给客户端 JavaScript 以使脚本能够把想绘制的东西都绘制到一块画布上. html的基本 ...

随机推荐

Django Croppie
下载 Django CroppieDjango Croppie django -croppie是一个简单集成croppie.js图像cropper到django项目的应用程序. 安装安装与pip安装 ...
【转载】可能是世界上最牛逼的网站统计程序——Matomo
大家做网站的时候一般都会使用网站统计程序.通常,国内网站会使用百度统计.CNZZ等,而国外网站则会使用Google Analytics等统计.国内的统计程序普遍功能不太丰富,且响应速度一般.Googl ...
List移除另外一个list的时候报错，java.lang.UnsupportedOperationException
问题编写代码的时候,使用Mybatis-plus分页查询返回的list,移除自己new的ArrayList报错根据异常信息,发现mybatis-plus分页查询返回的list底层并没有实现remo ...
两个多维高斯分布之间的KL散度推导
在深度学习中,我们通常对模型进行抽样并计算与真实样本之间的损失,来估计模型分布与真实分布之间的差异.并且损失可以定义得很简单,比如二范数即可.但是对于已知参数的两个确定分布之间的差异,我们就要通过推导 ...
kafka配置文件详解
kafka的配置分为 broker.producter.consumer三个不同的配置一 .BROKER 的全局配置最为核心的三个配置 broker.id.log.dir.zookeeper.con ...
c语言版去除源代码注释
去除代码中注释需要注意下面几点首先注释有"/*"开始到"*/"结束的多行或单行注释其次还有"//"这种单行注释另外还需要注意双引号和单 ...
jsoncpp笔记
Json Json是一种轻量级数据交换格式,可以表示数字,字符串,布尔值,null,数组,键值对: { "encoding" : "UTF-8", " ...
基于python常用排序与查找
""" 排序与查找 -- 冒泡排序 -- 选择排序 -- 快速排序 --****经典 -- 希尔排序 """ # 常用排序的实现 # 冒泡排 ...
【编程学习】浅谈哈希表及用C语言构建哈希表！
哈希表:通过key-value而直接进行访问的数据结构,不用经过关键值间的比较,从而省去了大量处理时间. 哈希函数:选择的最主要考虑因素--尽可能避免冲突的出现构造哈希函数的原则是: ①函数本身便于 ...
【思维】Luogu P3941 入阵曲
题目大意洛谷链接给出一个矩阵和 \(K\) ,问有多少子矩阵中的元素和能整除 \(K\). 数据范围 \(2\leq n,m\leq 400\),\(0\leq K\leq 10^6\). 思路 ...

canvas基础[一]探究出初中数学知识