梯度下降(Gradient descent)

首先，我们继续上一篇文章中的例子，在这里我们增加一个特征，也即卧室数量，如下表格所示：

因为在上一篇中引入了一些符号，所以这里再次补充说明一下：

x‘s：在这里是一个二维的向量，例如：x₁⁽ⁱ⁾第i间房子的大小(Living area)，x2^（i）表示的是第i间房子的卧室数量(bedrooms).

在我们设计算法的时候，选取哪些特征这个问题往往是取决于我们个人的，只要能对算法有利，尽量选取。

对于假设函数，这里我们用一个线性方程（在后面我们会说到运用更复杂的假设函数）：h_Θ(x) = Θ₀+Θ₁x₁+Θ₂x₂

这里，θ_i为参数，也称为权值（weights）。我们假定x₀= 1。因此上述可以表示为矩阵形式：

所以，对于我们给出的训练集，我们的任务就是怎么来学习得到Θ，从而使得我们的假设函数和我们给出的"正确答案"y更接近，也即，更好的拟合我们给出的数据。

为了来定义我们预测值和真实值之间的差异，我们引入代价函数(cost function)的概念

所以，现在我们的任务就是来求得一个Θ，从而使得代价函数达到最小，也即全局最小(global minimun).在这里我们使用梯度下降算法来求函数的最小值。

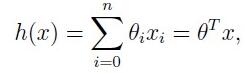
梯度下降法是按下面的流程进行的：

1）首先对θ赋值，这个值可以是随机的，也可以让θ是一个全零的向量。

2）改变θ的值，使得J(θ)按梯度下降的方向进行减少。

如下图：

上图表示的是参数Θ和代价函数J(Θ)的关系图，深蓝色为全局最小，浅蓝色为局部最小，红色则表示J(Θ)有一个较大的取值，而梯度下降算法就是我们给定一个初始的Θ值，然后按照梯度下降的原则不断更新Θ值，使得J(Θ)向更低的方向进行移动。算法的结束将是在θ下降到无法继续下降为止。上面两条线代表我们给定两个初值，我们发现一条到达局部最小，即浅蓝色，而一条到达全局最小，即深蓝色。所以从这里我们可以看出，初始值的选择对梯度下降的影响很大。

梯度下降的更新规则：

解释：描述：对 θ 赋值，使得 J(θ)按梯度下降最快方向进行，一直迭代下去，最终得到局部最小值。其中 α 是学习率（ learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。

对于梯度下降，我们再来直观的画出图像理解一下，J(Θ)的图像我们如下

求导的目的，基本上可以说取这个红点的切线，就是这样一条红色的直线，刚好与函数相切于这一点，让我们看看这条红色直线的斜率，就是这条刚好与函数曲线相切的这条直线，这条直线的斜率正好是这个三角形的高度除以这个水平长度，现在，这条线有一个正斜率，也就是说它有正导数，因此，我得到的新的 θ1， θ1 更新后等于 θ1 减去一个正数乘以 α。当Θ取到最小，J(Θ)最小，也即Θ不能小时算法结束。

对于α ，后面会讲到，这里先简单提下：

如果 α 太小了，即我的学习速率太小，结果就是只能这样像小宝宝一样一点点地挪动，去努力接近最低点，这样就需要很多步才能到达最低点，所以如果 α 太小的话，可能会很慢因为它会一点点挪动，它会需要很多步才能到达全局最低点。
如果 α 太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛，下一次迭代又移动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来越远，所以，如果 α 太大，它会导致无法收敛，甚至发散。

批量梯度下降算法(batch gradient descent)

当只有一个训练样本时，执行梯度下降算法（注意这里只是对Θ_j求导，所以最后乘上的是x_j）

所以针对一个训练样本，更新规则如下：

现在推广到存在多个特征时

注意：迭代都是需要同时进行的。

上面所说的就是批量梯度下降算法(batch gradient descent)，因为它的每次迭代都需要用到所有的训练样本，也即对所有的训练样本进行求和。当上式收敛时则退出迭代，何为收敛，即前后两次迭代的值不再发生变化了。一般情况下，会设置一个具体的参数，当前后两次迭代差值小于该参数时候结束迭代。

随机梯度下降算法(stochastic gradient descent)

当样本集数据量m很大时，由于每次在进行批量梯度下降时都需要用到所有的训练样本，所以开销就会很大，这个时候我们更多时候使用随机梯度下降算法(stochastic gradient descent),算法如下所示：

在进行随机梯度下降算法时，我们每次迭代都只选取一个训练样本，这样当我们迭代到若干样本的时候Θ就已经迭代到最优解了。

正规方程(The Normal equations)

梯度下降给我们提供了一种最小化J的方法，除了梯度下降，正规方程也是一种很好求解Θ的方法，这里只给出结论，如下