DAG的生成

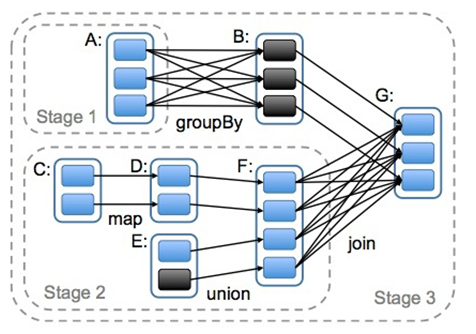
DAG(Directed Acyclic Graph) 叫做有向无环图，原始的RDD通过一系列的转换就形成了DAG，根据RDD之间的依赖关系的不同将DAG划分成不同的Stage，对于窄依赖，partition的转换处理在Stage中完成计算。对于宽依赖，由于有Shuffle的存在，只能在parent RDD处理完成后，才能开始接下来的计算，因此宽依赖是划分Stage的依据。

DAG的更多相关文章

  1. UVA103 dp基础题，DAG模型

    1.UVA103 嵌套n维空间 DAG模型记忆化搜索,或者 最长上升子序列. 2.dp[i]=max( dp[j]+1),(第i个小于第j个) (1) //DAG模型记忆化搜索 #include< ...

  2. JavaScript + SVG实现Web前端WorkFlow工作流DAG有向无环图

    一.效果图展示及说明 (图一) (图二) 附注说明: 1. 图例都是DAG有向无环图的展现效果.两张图的区别为第二张图包含了多个分段关系.放置展示图片效果主要是为了说明该例子支持多段关系的展现(当前也 ...

  3. CF721C. Journey[DP DAG]

    C. Journey time limit per test 3 seconds memory limit per test 256 megabytes input standard input ou ...

  4. [CF225C] Barcode (简单DAG上dp)

    题目链接:http://codeforces.com/problemset/problem/225/C 题目大意:给你一个矩阵,矩阵中只有#和.两种符号.现在我们希望能够得到一个新的矩阵,新的矩阵满足 ...

  5. 九、DAG hierarchy

    DAG 节点有两种,Transformation/shape. shape节点是transformation的子节点. transformation节点包括position, rotation, sc ...

  6. 02_嵌套矩形(DAG最长路问题)

    来源:刘汝佳<算法竞赛入门经典--训练指南> P60 问题2: 问题描述:有n个矩形,每个矩形可以用两个整数a,b描述,表示它们的长和宽.矩形X(a,b)可以嵌套在矩形Y(c,d)中的条件 ...

  7. 求DAG上两点的最短距离

    Problem 给出一个不带边权(即边权为1)的有向无环图(unweighted DAG)以及DAG上两点s, t,求s到t的最短距离,如果无法从s走到t,则输出-1. Solution DFS,BF ...

  8. DAG模型

    数字三角形: 1.递归计算 int solve(int i,int j) { :max(solve(i+,j),solve(i+,j+))); } 2.记忆化搜索,不用指明计算顺序,并且保证每个状态只 ...

  9. UVa 103 Stacking Boxes --- DAG上的动态规划

    UVa 103 题目大意:给定n个箱子,每个箱子有m个维度, 一个箱子可以嵌套在另一个箱子中当且仅当该箱子的所有的维度大小全部小于另一个箱子的相应维度, (注意箱子可以旋转,即箱子维度可以互换),求最 ...

  10. DAG上的动态规划之嵌套矩形

    题意描述:有n个矩形,每个矩形可以用两个整数a.b描述,表示它的长和宽, 矩形(a,b)可以嵌套在矩形(c,d)当且仅当a<c且b<d, 要求选出尽量多的矩形排成一排,使得除了最后一个外, ...

随机推荐

  1. Codecombat 游戏攻略（计算机科学三）

    第二关 赋值运算符-=字符串拼串循环语句while // 你可以把字符串连起来,或者把数字连接到字符串. // 一起唱歌,使用字符串连接: // X potions of health on the ...

  2. 支持向量机（四）----序列最小最优化算法SMO

    在支持向量机(二)和(三)中,我们均遗留了一个问题未解决,即如何求解原问题的对偶问题: 在支持向量机(二)中对偶问题为: 在支持向量机(三)中的对偶问题为: 对于上述两个对偶问题,我们在支持向量机(三 ...

  3. 关于vsftpd连接出现“响应: 530 Permission denied”的坑

    在设置vsftpd.conf文件中的变量 anonymous_enable=YES 需要使用用户进行登录,如果conf文件内缺少下列三行中的任何一行都需要补充完整,不然就会出现 “响应: 530 Pe ...

  4. spring boot 集成 mybatis 单元测试Dao层 控制台报错：org.apache.ibatis.binding.BindingException: Invalid bound statement (not found):

    最近帮同学做毕业程序,采用后端spring boot + mybatis + H2,将框架搭好进行各层的单元测试时,在dao层就出现了错,如图 于是在网上找各种资料,有的说是xml文件和接口没有一一对 ...

  5. spring- junit测试事务回滚

    http://blog.csdn.net/molingduzun123/article/details/49383235

  6. 《SQL Server 2012 T-SQL基础》读书笔记 - 1.背景

    几个缩写的全称:Data Definition Language (DDL), Data Manipulation Language (DML), and Data Control Language ...

  7. Linux shell - 修改文件所属用户和组 (chown, chgrp)

    在工作中,会遇到这样的情况,需要把目录所属的的root用户更改到普通用户,root组更改到普通组. sha-q:/ # ll drwxr-xr-x 2 root root 4096 2014-09-1 ...

  8. Android单行跑马灯效果实现

    参考网址:https://www.jianshu.com/p/e6c1b825d322 起初,使用了如下XML布局: <TextView android:id="@+id/tv_per ...

  9. mongoexport导出记录到csv文件

    root@service:~# mongoexport -d prod -c employees -f _id,platform,phone --csv -o /opt/employees.csv 2 ...

  10. Flask中的实例化配置

    也就是在app=Flask(__name__)括号中的参数 1.static_folder = 'static', # 静态文件目录的路径 默认当前项目中的static目录 2.static_url_ ...